Théorème de Sylvester–Gallai

Le théorème de Sylvester–Gallai affirme qu'étant donné un ensemble fini de points du plan, on a l'alternative suivante :

• soit tous les points sont colinéaires,
• soit il existe une droite qui contient exactement deux de ces points (droite ordinaire).

Ce théorème est issu d'un problème initialement posé par James Joseph Sylvester^[1], qui fut reposé indépendamment par Paul Erdős^[2]. Il fut résolu par Tibor Gallai (de) en 1944^[3], même si un théorème équivalent avait déjà été montré par Eberhard Melchior (en)^[4].

Ce théorème ne s'applique pas à des ensembles infinis de points : il suffit pour s'en convaincre de considérer l'ensemble des points de coordonnées entières dans le plan euclidien.

Les droites contenant exactement deux points sont nommées droites ordinaires. Un algorithme de Mukhopadhyay et al.^[5],[6] permet de trouver une droite ordinaire dans un ensemble de n points en temps O(n log n).

Point de vue projectif et problème dual

Le même problème peut être posé dans le plan projectif réel plutôt que dans le plan euclidien. Le problème projectif ne généralise en rien le problème euclidien, car tout ensemble fini de points projectifs peut être ramené à un ensemble de points du plan euclidien par une transformation conservant les droites ordinaires. Le point de vue projectif permet cependant de décrire plus naturellement et donc plus facilement certaines configurations, par exemple la configuration de McKee, décrite plus bas.

Par dualité projective, l'existence d'une droite ordinaire associée à un ensemble fini non colinéaire de points du plan projectif est équivalente à l'existence d'un point ordinaire, c'est-à-dire un point d'intersection d'exactement deux droites, dans un ensemble de droites qui ne passent pas toutes par un point commun.

Melchior a montré en 1940, avant la preuve de Gallai, que tout ensemble fini de droites non globalement concordantes présente au moins trois points ordinaires. Il s'est servi de la caractéristique d'Euler pour montrer que tout tel arrangement de droites a au moins trois sommets de degré 4 ; par dualité, tout ensemble de points non colinéaires possède donc au moins trois droites ordinaires.

Démonstration du théorème de Sylvester–Gallai

La preuve suivante^[7] est due à Leroy Milton Kelly (en)^[8] et repose sur la méthode de descente infinie.

Supposons donné un ensemble fini de points du plan, non colinéaires (en particulier, cet ensemble contient au moins trois points). Nous appellerons droite de connexion toute droite qui contient au moins deux points de l'ensemble. Il s'agit de montrer qu'au moins une de ces droites de connexion contient exactement deux points.

La grandeur utilisé pour la méthode de la descente infinie sera la distance minimale entre les droites de connexions et tout points extérieurs à celles-ci.

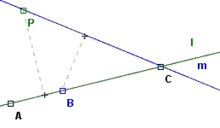
Supposons donc que notre ensemble de points n'est pas colinéaire, et soit (P,l) un point et une droite de connexion quelconques. Par hypothèse, l contient alors trois points, notés A, B et C. On suppose sans perte de généralité que le projeté orthogonal de P sur l se trouve entre A et B. Considérons alors la droite de connexion m passant par C et P. m est alors une droite de connexion qui ne contient pas B et la distance séparant B de m est strictement inférieure à la distance séparant P de l. En effet, si l'on considère les projections, le triangle rectangle hypoténuse BC est semblable à celui d'hypoténuse PC, et strictement inclut dans celui-ci.

Ainsi nous avons montré qu'il est toujours possible sous l'hypothèse initiale de trouver un point de notre ensemble avec une distance minimale aux droites de connexions strictement inférieur à un point donné. Ceci mène à une contradiction, puisque il y a un nombre fini de telles distances.

Généralisations du théorème de Sylvester–Gallai

Les deux configurations connues de n points présentant moins de n/2 droites ordinaires.

Si le théorème de Sylvester–Gallai affirme l'existence d'au moins une droite de connexion contenant exactement deux points (droite ordinaire), on ne connaît pas d'arrangement de points tel qu'il n'existe qu'une seule droite ordinaire ; le résultat de Melchior montre que, si les points ne sont pas tous alignés, il existe au moins trois droites ordinaires.

Ceci conduisit Gabriel Dirac à émettre la conjecture^[9] affirmant que pour tout ensemble de n points, non tous colinéaires, il existe au moins ⁿ⁄₂ droites ordinaires. En 2006, cette conjecture est démentie par seulement deux contre-exemples :

• Le premier, trouvé par Kelly et Moser^[10], est composé par les sommets, les milieux d'arêtes, et le centre d'un triangle équilateral ; ces sept points déterminent seulement trois droites ordinaires. La configuration dans laquelle ces trois droites ordinaires se confondent en une seule droite ne peut être réalisée dans le plan euclidien, mais forme un plan projectif fini connu sous le nom de plan de Fano.
• L'autre contre-exemple, imaginé par McKee^[11], est constitué des sommets de deux pentagones réguliers ayant une arête commune, du milieu de cette arête, et de quatre points à l'infini (c'est-à-dire situés sur la droite à l'infini dans le plan projectif). Ces 13 points déterminent 6 droites ordinaires. Il est possible de déformer cette configuration de manière à ramener tous les points dans le plan euclidien usuel.

Une version plus faible de la conjecture de Dirac a été prouvée par Csima et Sawyer^[12]. Elle énonce que dans n'importe quel ensemble de n points, il y a au moins droites ordinaires.

Un résultat proche du théorème de Sylvester–Gallai est le théorème de Beck (en), qui affirme qu'un ensemble de points du plan présente soit un grand nombre de droites de connexion, soit un grand sous-ensemble maximal de points colinéaires.

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article en anglais intitulé « Sylvester–Gallai theorem » (voir la liste des auteurs)

Voir aussi

• Théorème de De Bruijn–Erdős (géométrie d'incidence) (en)
• Théorème de Don Chakerian

• Portail de la géométrie