Théorème de Pappus

Ne doit pas être confondu avec Théorème de Pappus-Guldin.

Le théorème de Pappus est un théorème de géométrie projective plane qui possède plusieurs déclinaisons en géométrie affine. En géométrie projective Il s'énonce uniquement en termes d'alignements de points et d'intersections de droites, et se démontre dans n'importe quel plan projectif construit sur un corps commutatif.

Dans une approche axiomatique de la géométrie projective, il peut être pris comme axiome et caractérise alors, parmi les plans vus comme structure d'incidence, ceux qui peuvent être construit sur un corps commutatif, de même en géométrie affine pour l'avatar affine du théorème de Pappus (voir plan affine arguésien). Il a pour conséquence l'axiome de Desargues qui se déduit des axiomes d'incidence et de l'axiome de Pappus par le théorème de Hessenberg.

Sommaire

1 Énoncé du théorème
2 Démonstration à l'aide des applications projectives
3 Démonstration en géométrie affine par le théorème de Ménélaüs
4 Notions connexes
5 Sources

Énoncé du théorème

Théorème de Pappus

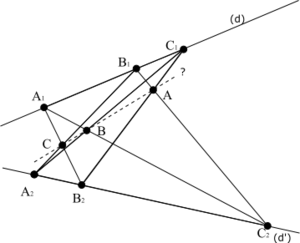
Dans un plan, soient $A 1$ , $B 1$ , $C 1$ trois points distincts alignés sur une droite $(d)$ , et soient $A 2$ , $B 2$ , $C 2$ trois autres points distincts alignés sur une autre droite $(d^\prime)$ alors les points

$A$ intersection de $(B 2 C 1)$ avec $(C 2 B 1)$
$B$ intersection de $(A 2 C 1)$ avec $(C 2 A 1)$
$C$ intersection de $(A 2 B 1)$ avec $(B 2 A 1)$

sont alignés.

Il s'agit d'un théorème de géométrie projective donc les points considérés peuvent être propres ou impropres. Dans le cas où tous les points sont propres, on obtient une configuration du type ci-contre.

Remarques :

si l'on note $(Δ)$ la droite portant les points A,B,C alors les assertions suivantes sont équivalentes (en géométrie projective) :

-- les trois droites $(d)$ , $(d^\prime)$ et $(Δ)$ sont concourantes ;

-- les trois droites $(A 1 A 2)$ $(B 1 B 2)$ $(C 1 C 2)$ sont concourantes ;

-- les six droites « croisillons » $(B 2 C 1)$ $(C 2 B 1)$ $(A 2 C 1)$ $(C 2 A 1)$ $(A 2 B 1)$ $(B 2 A 1)$ sont tangentes à une même conique.

-- Les deux droites $(d)$ et $(d^\prime)$ peuvent être considérées comme une conique dégénérée : pour l'hexagramme $A 1 B 2 C 1 A 2 B 1 C 2$ , le théorème de Pappus-Pascal affirme l'alignement des points $A$ , $B$ et $C$ .

Démonstration à l'aide des applications projectives

Démonstration du théorème

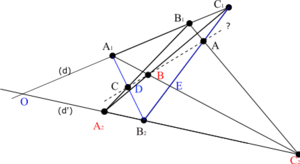
On construit les points O intersection de (d) et (d'), D intersection de $(A 1 B 2)$ et $(A 2 C 1)$ et E intersection de $(A 1 C 2)$ et $(C 1 B 2)$

On considère la projection centrale p de la droite $(A 1 B 2)$ sur la droite (d) de centre $A 2$

$A 1$ a pour image $A 1$
C a pour image $B 1$
D a pour image $C 1$
$B 2$ a pour image O

On considère la projection centrale q de la droite (d) sur la droite $(B 2 C 1)$ de centre $C 2$

$A 1$ a pour image E
$B 1$ a pour image A
$C 1$ pour image $C 1$
O a pour image $B 2$

Par l'application projective q o p de la droite $(A 1 B 2)$ sur la droite $(B 2 C 1)$

$A 1$ a pour image E
C a pour image A
D a pour image $C 1$
$B 2$ a pour image $B 2$

Si on regarde maintenant la projection centrale r de la droite $(A 1 B 2)$ sur la droite $(B 2 C 1)$ de centre B

$A 1$ a pour image E
D a pour image $C 1$
$B 2$ a pour image $B 2$

Or, une application projective d'une droite sur une autre est entièrement déterminée par l'image de trois points distincts. Les transformations q o p et r coïncident sur $A 1$ , D et $B 2$ . Elles sont donc égales et $r (C) = A$ . Les points A, B et C sont donc alignés.

Démonstration en géométrie affine par le théorème de Ménélaüs

Démonstration du théorème de Pappus à l'aide de Ménélaüs

Le théorème a plusieurs avatars affines qui se déduisent chacun de la version projective par choix d'une droite à l'infini. On suppose ici comme ci-dessus que les 2 triplets de points distincts ( $A 1$ , $B 1$ , $C 1$ ) d'une part, ( $A 2$ , $B 2$ , $C 2$ ) d'autre part, sont chacun alignés sur deux droites distinctes. On ajoute comme condition que $(B 2 C 1)$ et $(C 2 B 1)$ sont sécantes (en A), ainsi que $(A 2 C 1)$ et $(C 2 A 1)$ (en B), et que $(A 2 B 1)$ et $(B 2 A 1)$ (en C). On en déduit par le théorème de Pappus que A, B et C sont alignés.

En voici une démonstration directe en géométrie affine, moyennant quelques conditions supplémentaires, à savoir que $(A 2 B 1)$ et $(B 2 C 1)$ sont sécantes en $J 1$ , $(B 2 C 1)$ et $(A 1 C 2)$ en $L 1$ , $(A 2 B 1)$ et $(A 1 C 2)$ en $K 1$ .

Les trois points ainsi définis sont alors distincts et non alignés et définissent le triangle (en bleu sur la figure) $J 1 K 1 L 1$ .

la droite $(A 1 C 1)$ intersecte les trois côtés du triangle en $A 1$ , $B 1$ , $C 1$
la droite $(A 2 C 2)$ intersecte les trois côtés du triangle en $A 2$ , $B 2$ , $C 2$
la droite $(B 1 C 2)$ intersecte les trois côtés du triangle en $B 1$ , $A$ , $C 2$
la droite $(A 2 C 1)$ intersecte les trois côtés du triangle en $A 2$ , $B$ , $C 1$
la droite $(A 1 B 2)$ intersecte les trois côtés du triangle en $A 1$ , $C$ , $B 2$

D'après Ménélaüs, ces alignements se traduisent par les égalités suivantes :

$\frac{\overline{A_1K_1}}{\overline{A_1L_1}}\times \frac{\overline{B_1J_1}}{\overline{B_1K_1}} \times \frac{\overline{C_1L_1}}{\overline{C_1J_1}} = 1$

$\frac{\overline{A_2J_1}}{\overline{A_2K_1}}\times \frac{\overline{B_2L_1}}{\overline{B_2J_1}} \times \frac{\overline{C_2K_1}}{\overline{C_2L_1}} = 1$

$\frac{\overline{B_1K_1}}{\overline{B_1J_1}}\times \frac{\overline{AJ_1}}{\overline{AL_1}} \times \frac{\overline{C_2L_1}}{\overline{C_2K_1}} = 1$

$\frac{\overline{A_2K_1}}{\overline{A_2J_1}}\times \frac{\overline{BL_1}}{\overline{BK_1}} \times \frac{\overline{C_1J_1}}{\overline{C_1L_1}} = 1$

$\frac{\overline{A_1L_1}}{\overline{A_1K_1}}\times \frac{\overline{CK_1}}{\overline{CJ_1}} \times \frac{\overline{B_2J_1}}{\overline{B_2L_1}} = 1$

En multipliant membre à membre ces cinq égalités, il reste après simplification :

$\frac{\overline{AJ_1}}{\overline{AL_1}}\times \frac{\overline{BL_1}}{\overline{BK_1}} \times \frac{\overline{CK_1}}{\overline{CJ_1}} = 1$

ce qui prouve d'après la réciproque de Ménélaüs l'alignement des trois points $A$ , $B$ et $C$ .

Une démonstration analogue peut être faite, en modifiant les conditions supplémentaires, avec le triangle $J 2 K 2 L 2$ (en rouge sur la figure). Dans ce cas, les trois droites $(B 1 C 2)$ , $(A 2 C 1)$ et $(A 1 B 2)$ (en rouge sur la figure) échangent leur rôle avec les trois droites $(B 2 C 1)$ , $(A 1 C 2)$ et $(A 2 B 1)$ (en bleu sur la figure).

On déduit la version projective du théorème de Pappus de cette version affine en choisissant judicieusement dans le plan projectif une droite à l'infini, pour se ramener au plan affine de façon à vérifier toutes les conditions du théorème démontré par Ménélaüs.

Notions connexes

Le théorème de Hessenberg fait le lien entre le théorème de Pappus et le théorème de Desargues.
Le théorème de Pappus affine dans le plan affine.
L'hexagramme de Pascal dont la configuration de Pappus est une version dégénérée (la conique est une bidroite).
Graphe de Pappus
Enfin il est indispensable de rappeler que la configuration de Pappus est un bel exemple de dualité.

Sources

Leçons de géométrie projective de F. Enriqués
Petite encyclopédie de mathématiques Ed. Didier
Enfin un site où sont donnés de nombreux développements sur le Thèorème de Pappus:Merveilleux Pappus

v · Géométrie projective

Plan projectif · Plan projectif (structure d'incidence) · Plan projectif arguésien · Théorème de Pappus · Théorème de Desargues · Dualité · Théorème de Hessenberg · Théorème fondamental de la géométrie projective · Hexagramme de Pascal · Conique · Construction d'un cercle point par point · Construction d'une parabole tangente par tangente · Plan de Fano · Rapport anharmonique · Division harmonique · Application projective · Fonction homographique · Perspective · Perspective conique · Géométrie · Géométrie analytique · Géométrie synthétique

Portail de la géométrie

Catégories :

Théorème de géométrie
Géométrie projective
Ligne droite

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème de Pappus de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Theoreme de Pappus — Théorème de Pappus Sommaire 1 Introduction 2 Énoncé du théorème 3 Démonstration à l aide des applications projectives 4 Notions connexes … Wikipédia en Français
Théorème de pappus — Sommaire 1 Introduction 2 Énoncé du théorème 3 Démonstration à l aide des applications projectives 4 Notions connexes … Wikipédia en Français
Théorème de Pappus-Guldin — Théorème de Guldin On désigne sous le nom de théorème de Guldin deux énoncés de géométrie euclidienne établis par le mathématicien suisse Paul Guldin. Il est probable que ces résultats aient déjà été connus de Pappus d Alexandrie et c est… … Wikipédia en Français
Théorème de Desargues — dans un plan projectif : les deux triangles (non plats) ABC et A B C ont leurs sommets sur 3 droites distinctes p = (AA ) , q = (BB ) et r = (CC ) ; alors ces 3 droites sont concourantes (en S) si et seulement si les points P = (BC) ∩… … Wikipédia en Français
Theoreme d'Hessenberg — Théorème d Hessenberg En géométrie projective, le théorème d’Hessenberg fait le lien entre le théorème de Pappus et le théorème de Desargues. On s’intéresse ici au théorème d Hessenberg dans sa version projective (il existe également une version… … Wikipédia en Français
Théorème d'Hessenberg — En géométrie projective, le théorème d’Hessenberg fait le lien entre le théorème de Pappus et le théorème de Desargues. On s’intéresse ici au théorème d Hessenberg dans sa version projective (il existe également une version affine qui s en déduit … Wikipédia en Français
Théorème de Hessenberg — Théorème d Hessenberg En géométrie projective, le théorème d’Hessenberg fait le lien entre le théorème de Pappus et le théorème de Desargues. On s’intéresse ici au théorème d Hessenberg dans sa version projective (il existe également une version… … Wikipédia en Français
Théorème d’Hessenberg — Théorème d Hessenberg En géométrie projective, le théorème d’Hessenberg fait le lien entre le théorème de Pappus et le théorème de Desargues. On s’intéresse ici au théorème d Hessenberg dans sa version projective (il existe également une version… … Wikipédia en Français
Theoreme de Thales — Théorème de Thalès Pour l’article homonyme, voir Théorème de Thalès (cercle). Configuration possible du théorème Le théorème de Thalès ou théorè … Wikipédia en Français
Théorème de Thales — Théorème de Thalès Pour l’article homonyme, voir Théorème de Thalès (cercle). Configuration possible du théorème Le théorème de Thalès ou théorè … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème de Pappus

Sommaire

Énoncé du théorème

Démonstration à l'aide des applications projectives

Démonstration en géométrie affine par le théorème de Ménélaüs

Notions connexes

Sources

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Théorème de Pappus

Sommaire

Énoncé du théorème

Démonstration à l'aide des applications projectives

Démonstration en géométrie affine par le théorème de Ménélaüs

Notions connexes

Sources

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link