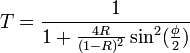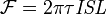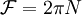Interféromètre de fabry-pérot

Simulation informatique d'une figure d'interférences d'un interféromètre de Fabry-Perot.

L'interféromètre de Fabry-Perot est un interféromètre optique constitué de deux surfaces partiellement réfléchissantes planes à hauts coefficients de réflexion (souvent supérieurs à 95 %).

La lumière entrante effectue de multiples aller-retour à l'intérieur de cette cavité, et ressort partiellement à chaque réflexion. Les différents rayons lumineux sortants interfèrent entre eux, donnant lieu à une figure d'interférences à ondes multiples constituée d'anneaux concentriques fins.

Principe de l'interféromètre pour une onde monochromatique

Schéma de principe d'un interféromètre de Fabry-Perot : les rayons lumineux sont réfléchis à l'intérieur de la cavité, et en ressortent partiellement.

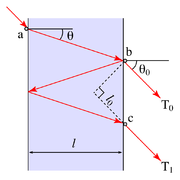
Pour simplifier l'étude, on suppose que l'interféromètre est éclairé par une source de lumière monochromatique. On peut représenter, comme sur la figure ci-contre, un rayon en particulier, et calculer sa contribution à la lumière sortante.

Les rayons lumineux sortant par la deuxième surface aux points b et c n'ont pas parcouru la même longueur de trajet (ou chemin optique). Ainsi, ils présentent un déphasage φ l'un par rapport à l'autre, dépendant de l'angle θ. Ces deux rayons interfèrent entre eux ainsi qu'avec tous les autres rayons qui auront été réfléchis plusieurs fois entre les deux surfaces réfléchissantes. On peut alors montrer que, selon la valeur de θ, le rayon est transmis ou pas.

On s'aperçoit en fait que seules quelques valeurs de θ permettent de transmettre la lumière du rayon incident. Chacune de ces valeurs peut être directement visualisée : elles correspondent à une série d'anneaux concentriques observés sur la figure d'interférence. En effet, en plaçant une lentille convergente à la sortie de l'interféromètre, tous les rayons faisant le même angle θ par rapport à l'axe central de la lentille formeront un anneau.

Plus précisément, la transmittance est donnée par l'expression suivante :

dans laquelle 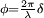avec 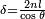la différence de marche subie par la lumière après un aller-retour dans l'étalon, R le coefficient de réflexion de chaque interface,n l'indice de réfraction du milieu présent entre les deux surfaces réfléchissantes et θ l'angle d'incidence interne.

Cette formule donne la figure d'interférence présentée en début d'article.

Transmission en fonction de la longueur d'onde

Courbes de la transmittance T de l'interféromètre de Fabry-Pérot en fonction de la longueur d'onde.

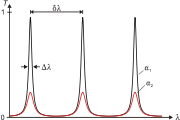
La figure d'interférence obtenue présente toujours des anneaux concentriques, mais leur taille varie en fonction de la distance entre les deux surfaces réfléchissantes, et de la longueur d'onde de la lumière utilisée. En effet, lorsqu'on étudie la formule précédente on s'aperçoit que seules quelques longueurs d'ondes sont transmises : la transmittance en fonction de λ présente des pics séparés de δλ et d'une largeur Δλ

Cette courbe varie en fonction de l'angle θ : à chaque longueur d'onde correspond un système d'anneaux. Et en présence de plusieurs longueurs d'ondes, on peut comparer ces différents systèmes d'anneaux afin de mesurer les longueurs d'ondes. Cet interféromètre est donc utilisé en spectrométrie.

Finesse de l'interféromètre

Courbe représentant la finesse d'un interféromètre de Fabry-Pérot en fonction du coefficient de réflexion des miroirs formant la cavité.

Pour pouvoir mieux séparer les différents anneaux, il est intéressant qu'ils soient les plus fins possibles. On peut montrer que cela est équivalent à affiner les pics de la courbe précédente, c'est-à-dire à réduire Δλ par rapport à δλ. Ainsi, un interféromètre de bonne qualité présentera un Δλ beaucoup plus faible que δλ.

Pour simplifier, on utilise la grandeur suivante, appelée finesse :

.

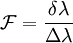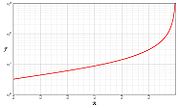
Et donc, plus la finesse est importante, plus les anneaux sont fins. Afin d'augmenter cette finesse, il est possible de rendre les surfaces formant la cavité très réfléchissantes. En effet, on peut montrer, comme l'illustre la courbe ci-contre, que la finesse augmente avec le coefficient de réflexion des surfaces.

Ainsi les interféromètre de Fabry-Pérot dans le commerce peuvent avoir des finesses valant quelques dizaines voire quelques centaines. En recherche on peut même aller jusqu'à quelques centaines de milliers.

Cette finesse élevée est un atout important de ce type d'interféromètres par rapport à l'interféromètre de Michelson, qui a une finesse de 2.

La finesse peut-être reliée au temps de vie des photons dans la cavité τ et à l'intervalle spectral libre en fréquence ISL :

Ainsi, le nombre d'oscillations N effectuées par la lumière dans la cavité est d'autant plus grand que la finesse est élevée :

Applications

Les utilisations possibles sont :

• dans le domaine de la spectroscopie (séparation de longueurs d'ondes très voisines)
• la réalisation de filtres interférentiels très sélectifs (ne laissant passer qu'une plage de longueurs d'ondes de l'ordre de 10 nm).
• la réalisation de cavités laser, les miroirs ne sont plus plans mais concaves afin de limiter au maximum les pertes
• le contrôle de la longueur d'onde des signaux pour certaines télécommunications.

Référence

• G. Hernandez, Fabry-Pérot Interferometers, Cambridge University Press, Cambridge, 1986 (ISBN 0-521-32238-3) 

• Portail de l’astronomie
• Portail de la physique