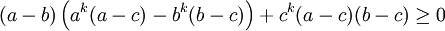Inegalite de Schur
- Inegalite de Schur
-
Inégalité de Schur
L'inégalité de Schur est une inégalité utilisée en théorie des nombres.
Enoncé
Soit a,b,c des nombres réels positifs et k un réel, alors on a:
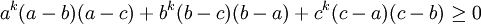
avec égalité si et seulement si a = b = c
Preuve
Quitte à permuter les variables, on peut choisir d'écrire 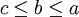 (de par la symétrie de la précédente inégalité). En arrangeant les termes, l'inégalité à démontrer est équivalente à :
(de par la symétrie de la précédente inégalité). En arrangeant les termes, l'inégalité à démontrer est équivalente à :
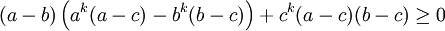
Cette dernière inégalité est immédiate car tous les termes à gauche sont positifs.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Inegalite de Schur de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Inégalité De Schur — L inégalité de Schur est une inégalité utilisée en théorie des nombres. Enoncé Soit a,b,c des nombres réels positifs et k un réel, alors on a: avec égalité si et seulement si a = b = c Preuve Quitte à permuter les variables, on peut choisir d… … Wikipédia en Français
Inégalité de schur — L inégalité de Schur est une inégalité utilisée en théorie des nombres. Enoncé Soit a,b,c des nombres réels positifs et k un réel, alors on a: avec égalité si et seulement si a = b = c Preuve Quitte à permuter les variables, on peut choisir d… … Wikipédia en Français
Inégalité de Schur — L inégalité de Schur est une inégalité utilisée en théorie des nombres. Enoncé Soit a,b,c des nombres réels positifs et k un réel, alors on a: avec égalité si et seulement si a = b = c Preuve Quitte à permuter les variables, on peut choisir d… … Wikipédia en Français
Schur — Issai Schur Issai Schur, né à Moguilev le 10 janvier 1875 et mort à Tel Aviv le 10 janvier 1941, est un mathématicien russe qui a surtout travaillé en Allemagne. Il a étudié à Berlin sous Frobenius, a obtenu son doctorat en 1901 et est devenu… … Wikipédia en Français
Issai Schur — Issai Schur, né à Moguilev le 10 janvier 1875 et mort à Tel Aviv le 10 janvier 1941, est un mathématicien russe qui a surtout travaillé en Allemagne. Il a étudié à Berlin sous Frobenius, a obtenu son doctorat en 1901 et est… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Théorie des équations (mathématiques) — Pour les articles homonymes, voir Théorie des équations. La théorie des équations est la partie des mathématiques qui traite des problèmes posés par les équations polynomiales de tous les degrés. Se trouvent ainsi rassemblés les problèmes de… … Wikipédia en Français
Axiomes d'Euclide — Géométrie euclidienne Euclide. La géométrie euclidienne commence avec les Éléments d Euclide, qui est à la fois une somme des connaissances géométriques de l époque et une tentative de formalisation mathématique de ces connaissances. Les notions… … Wikipédia en Français
Geometrie euclidienne — Géométrie euclidienne Euclide. La géométrie euclidienne commence avec les Éléments d Euclide, qui est à la fois une somme des connaissances géométriques de l époque et une tentative de formalisation mathématique de ces connaissances. Les notions… … Wikipédia en Français
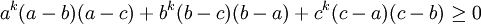
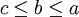 (de par la symétrie de la précédente inégalité). En arrangeant les termes, l'inégalité à démontrer est équivalente à :
(de par la symétrie de la précédente inégalité). En arrangeant les termes, l'inégalité à démontrer est équivalente à :