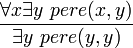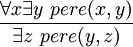Dictum de omni

En logique, l'instanciation universelle (également appelée Dictum de omni) est une règle d'inférence qui permet, à partir d'une vérité sur l'ensemble des membres d'une classe d'entités, d'inférer une vérité sur une entité particulière de cette classe. Elle est généralement considérée comme une règle de quantification pour le quantificateur universel, mais elle peut également être énoncée en tant qu'axiome. C'est l'un des principes de bases de la théorie de la quantification.

Exemple : « Tous les hommes sont mortels. Socrate est un homme. Donc Socrate est mortel. »

Sommaire 1 Définition formelle 2 Problème de la capture de variable 3 Instanciation universelle et systèmes de déduction 4 Notes et références de l'article 5 Voir aussi 5.1 Articles connexes

Définition formelle

De manière symbolique, la représentation de cette règle en tant que schéma d'axiome est :

(∀x A(x)) → A(a/x), avec la condition que a soit librement substituable à x dans A.

où a est un terme, et où A(a/x), appelé « substitution uniforme de x par a dans A » est le résultat de la substitution de toute occurrence libre de x dans A par a. La représentation en tant que règle d'inférence est :

Si ⊢ ∀x A alors ⊢ A(a/x)      ou     

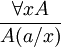
Problème de la capture de variable

Il faut prendre garde au cas où a est un terme qui contient des variables qui apparaissent liées dans A; si une occurrence de x apparait dans A dans le champ d'une de ces quantifications, la substitution « naïve » est fausse. C'est le phénomène dit de capture de variable. On a plusieurs solutions. Si la substitution est la substitution naïve, il faut interdire les substitutions avec capture de variable. C'est une solution qui fonctionne théoriquement, mais qui demande par exemple une règle de renommage des variables liées. On peut travailler également (il y a plusieurs façons de le réaliser) sur des formules à renommage des variables liées près, c'est-à-dire que l'on modifie la substitution pour qu'elle renomme les variables liées de façon satisfaisante en cas de capture de variables. La substitution n'est alors plus le simple remplacement d'occurrences d'une même lettre par un mot, mais tient compte de la structure logique de la formule.

L'exemple suivant illustre le phénomène de capture de variable. Dans la formule 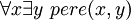, la variable x apparait dans le champ du quantificateur y. Si l'on souhaite substituer un terme a qui contient y, par exemple y lui-même, et que l'on utilise la substitution naïve, on a la dérivation suivante qui est erronée :

La prémisse dit que tout individu x a un père y (qui dépend de x). La dérivation erronée conclut que l'individu y est son propre père, ce qui ne découle évidemment pas de la première affirmation. L'erreur vient du fait qu'il n'est pas permis de substituer directement y (ou un terme qui contiendrait y) à x, car dans la prémisse, x apparait dans le champ du quantificateur existentiel sur y, et donc y, au lieu d'être une variable libre de la conclusion, se trouve capturée par ce quantificateur.

Une déduction correcte est, à renommage des variables liées près :

Instanciation universelle et systèmes de déduction

L'instanciation universelle est réalisée par la règle d'élimination de la déduction naturelle (énoncée indépendamment par Gerhard Gentzen et Stanislaw Jaskowski en 1934)^[1]. C'est en quelque sorte un cas particulier de la règle gauche du quantificateur universel dans le calcul des séquents du même Gentzen. On la réalise souvent par un schéma d'axiomes dans un système à la Hilbert.

Notes et références de l'article

• (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Universal instantiation ».

Voir aussi

Articles connexes

• Modus ponens
• Modus tollens

• Portail de la logique