Diagramme de venn

Les diagrammes d'Euler, de Venn, de Carroll, sont des schémas géométriques utilisés pour représenter des relations logico-mathématiques. Créés pour visualiser la structure logique des syllogismes, ils sont couramment utilisés pour l'étude des relations entre ensembles.

Sommaire 1 Diagrammes d'Euler 2 Diagrammes de Venn 2.1 Exemple de représentation d'un syllogisme (Barbara) par diagramme de Venn 3 Diagrammes de Carroll 3.1 Exemple de représentation d'un syllogisme (Barbara) par diagramme de Carroll 4 Source bibliographique

Diagrammes d'Euler

En vue d'étudier systématiquement les syllogismes, Leonhard Euler (1707-1783) eut l'idée de représenter géométriquement les attributs (ou propriétés, ou termes d'un syllogisme) : à chacun il associa un cercle, dont l'intérieur représentait l'extension (le domaine de validité) de l'attribut. La prise en compte simultanée de deux attributs (pour représenter une prémisse par exemple) conduisait à envisager trois configurations possibles :

---

---

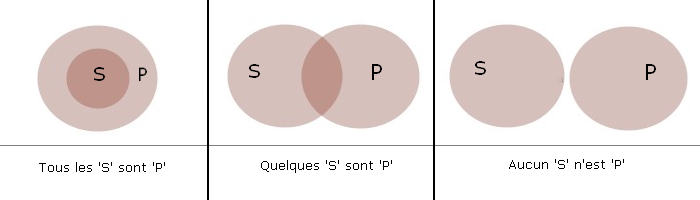
Pour trois attributs, situation à prendre en compte pour un syllogisme, le nombre configurations était de l'ordre d'une quinzaine, voire nettement plus si on prend en compte l'ordre des termes en vue d'une utilisation syllogistique. Exemples de configurations à valeur syllogistique :

---

---

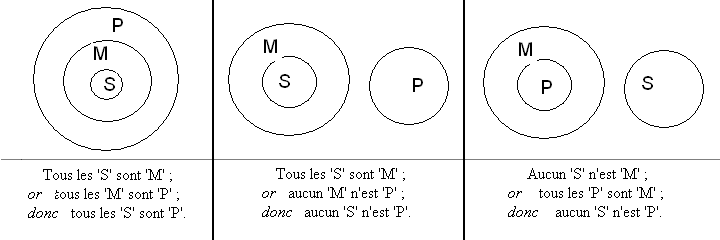
Exemples de configurations non syllogistiques :

---

---

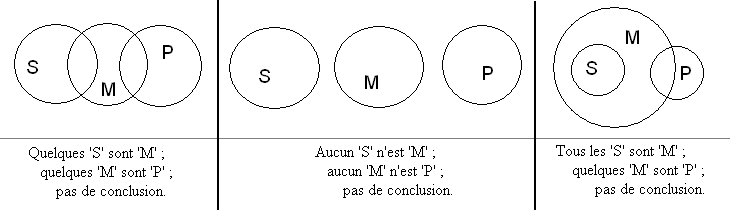
Certaines configurations à quatre attributs (ou plus) ne peuvent pas être représentées par la méthode d'Euler. Par exemple, quatre cercles ne peuvent pas avoir toutes leurs intersections (deux à deux, trois à trois, et quatre) disjointes.

Les "diagrammes d'Euler" sont couramment utilisés pour représenter les positions relatives de plusieurs ensembles (inclusion, intersection, disjonction).

Diagrammes de Venn

Un siècle plus tard, John Venn (1834-1923) opéra plusieurs modifications importantes dans la représentation eulérienne des attributs :

• remplacement des cercles par des courbes fermées simples (sans points doubles ; par exemple des ellipses)
• utilisation dans tous les cas d'une unique représentation pour chaque ensemble de n attributs, dans laquelle toutes les conjonctions possibles p à p des attributs existent
• coloration (grisé ou hachures) des régions connues comme « vides » (conjonctions qu'on sait impossibles)
• indication par un signe graphique des régions connues comme « non vides » (conjonctions qu'on sait possibles)

Ainsi les trois configurations d'Euler pour le cas de deux attributs deviennent :

---

---

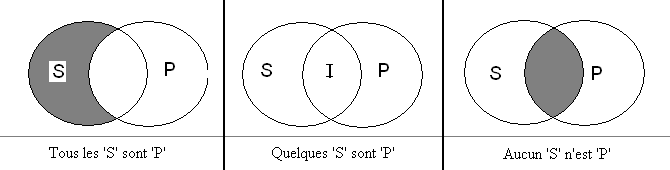
Venn pouvait représenter toutes les configurations associées à quatre attributs, voire cinq en trichant quelque peu avec ses principes (une zone centrale devait être considérée comme « extérieure »). Sa méthode fut étendue un siècle plus tard à six attributs par A. W. F. Edwards dans son livre Cogwheels of the Mind. Les diagrammes qui suivent sont créés à partir de ses travaux :

---

Diagramme d'Edwards-Venn à trois ensembles	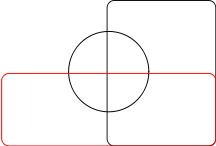	Diagramme d'Edwards-Venn à quatre ensembles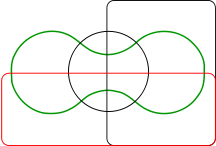
Diagramme d'Edwards-Venn à cinq ensembles	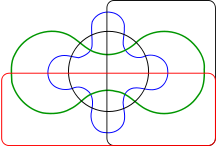	Diagramme d'Edwards-Venn à six ensembles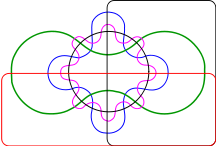
Source : Ian Stewart, Another Fine Math You've Got Me Into, 1992, chap. 4.

---

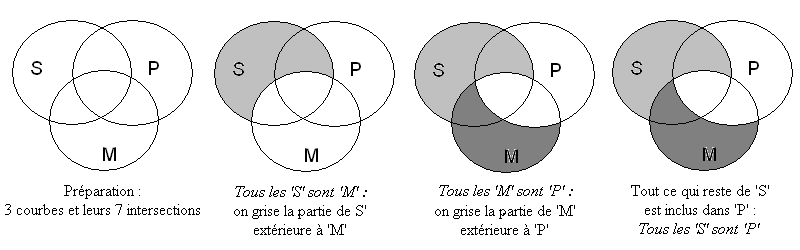
Exemple de représentation d'un syllogisme (Barbara) par diagramme de Venn

---

---

Diagrammes de Carroll

Contemporain de Venn, Lewis Carroll (1832-1898) refusait la dissymétrie posée a priori entre l'intérieur et l'extérieur, c'est-à-dire entre l'attribut et sa négation. Ainsi pour Carroll l'attribut mortel et l'attribut immortel ont la même valeur, et il n'est pas légitime que l'un soit représenté par un espace clos et l'autre par un espace non clos. Il proposa donc une représentation dans laquelle l'"univers" est un carré, et chaque attribut divise ce carré en deux parties égales. Dès lors deux attributs divisent l'univers en quatre, trois attributs en huit, et ainsi de suite.

---

---

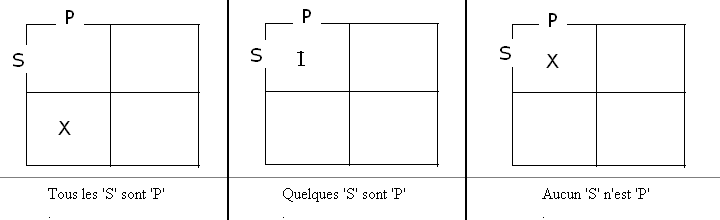
Renonçant à la connexité des subdivisions, Carroll pouvait représenter jusqu'à huit attributs simultanés. Par ailleurs il conservait le principe de Venn de signaler les régions connues comme vides et celles connues comme non vides. Les trois configurations d'Euler pour n=2 deviennent pour Carroll :

---

---

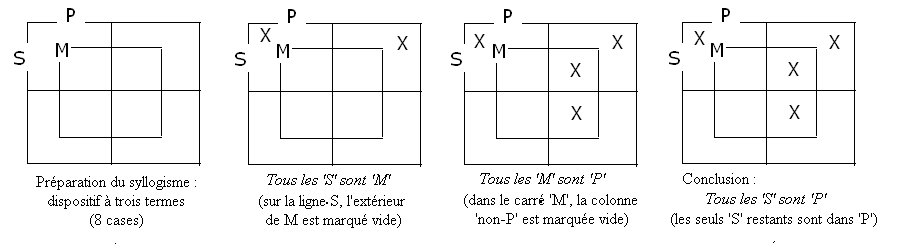
Exemple de représentation d'un syllogisme (Barbara) par diagramme de Carroll

---

---

Source bibliographique

• Jean Gattegno et Ernest Coumet, Logique sans peine, éd. Hermann, 1966. Traduction française (partielle) de l'ouvrage Symbolic Logic publié par Lewis Carroll en 1896-97 ; contient des références à l'ouvrage Symbolic Logic de Venn.

• Portail des mathématiques