Crible d'Erathostène

Le crible d'Ératosthène est un procédé qui permet de trouver tous les nombres premiers inférieurs à un certain entier naturel donné N. C'est l'ancêtre du crible d'Atkin qui est plus rapide mais plus complexe.

Algorithme

L'algorithme procède par élimination : il s'agit de supprimer d'une table tous les multiples des entiers de 2 à N.

À la fin du processus, tous les entiers qui n'ont pas été rayés sont les nombres premiers inférieurs à N.

L'animation ci-dessous illustre le crible d'Eratosthène pour N=120 :

Voici, étape par étape, le détail de la mise en œuvre de l'algorithme pour N=20.

Étape 1. Écrivons la liste des nombres naturels compris entre 2 et 20

Étape 2. On marque le nombre suivant non rayé de la liste, comme premier.

Étape 3. On raye dans la liste, tous les multiples du nombre que l'on vient d'entourer.

Étape 4. Si le carré du nombre suivant non rayé est inférieur à 20, alors on recommence à l'étape 2 sinon on déclare tous les entiers restants non rayés premiers.

Puisque 3 élevé au carré est inférieur à 20, on retourne à l'étape 2 :

À l'étape 4, l'entier suivant non rayé 5 a un carré strictement supérieur à 20, on considère comme premiers tous les entiers suivants non rayés.

Résultat : Les entiers premiers compris entre 2 et 20 sont : 2, 3, 5, 7, 11, 13, 17, 19.

Pour obtenir les entiers premiers inférieurs à N=99, on raye dans l'ordre tous les multiples des nombres premiers p=2, 3, 5, 7, … à partir de p² jusqu'à N. On s'arrête lorsque l'entier premier p suivant vérifie p² > N (Si un entier non premier est strictement supérieur à 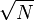alors il a au moins un diviseur inférieur à 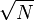et aura donc déjà été rayé). On va donc aller jusqu'à p=9, parce que 10²=100>99, et déclarer premiers tous les entiers non rayés suivants. On obtient la table suivante :

Exemple d'implémentation

Le crible d'Eratothène s'implémente facilement avec une fonction récursive, qu'il suffit d'appeler initialement avec le tableau des entiers de 2 à N.

Voici un exemple de code en bash :

erat()
if (($1**2 > ${!#}));
then
    echo $@;
else
    a=$1; b="";
    while shift; (($#));
    do (($1%$a)) && b+=" "$1;
    done;
    echo $a $(erat $b);
fi
 
erat {2..1000}

Notes et références

Κόσκινον Ερατοσθένους or, The Sieve of Eratosthenes. Being an Account of His Method of Finding All the Prime Numbers, by the Rev. Samuel Horsley, F. R. S., Philosophical Transactions (1683-1775), Vol. 62. (1772), pp. 327-347.

Liens internes

• Crible d'Atkin

Liens externes

• Animation interactive (JavaScript)
• Crible d'Ératosthène (Java)

• Portail des mathématiques