Clause de horn

Clause de horn

Clause de Horn

Page d'aide sur l'homonymie Pour les articles homonymes, voir Horn.

La dénomination « clause de Horn » vient du nom du logicien Alfred Horn qui, le premier, met en évidence l’intérêt de telles clauses en 1951 dans l’article « On sentences which are true of direct unions of algebras » publié dans le Journal of Symbolic Logic, numéro 16, pages 14 à 21.

Sommaire

Définition

En logique, en particulier en calcul propositionnel, une clause de Horn est une clause comportant au plus un littéral positif.

Il existe donc trois types de clauses de Horn :

De plus toute clause de Horn est de la forme 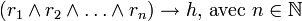(r_{1} \land r_{2} \land \ldots \land r_{n}) \rightarrow h \text{, avec } n \in \mathbb{N} . Les clauses de Horn forment un sous–ensemble des formes normales disjonctives dans lesquelles un seul terme est positif.

Interprétation intuitive

Que peut–on représenter avec des clauses de Horn ?

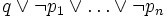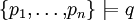  • Les clauses de Horn strictes q \lor \lnot p_{1} \lor \ldots \lor \lnot p_{n} sont équivalentes à \{ p_{1} \text{,} \ldots \text{,} p_{n} \} \models q.
    Intuitivement, elles représentent des règles « si ... alors ... » et permettent de déduire de nouveaux faits à partir de faits existants ;
  • Les clauses de Horn positives sont appelées faits. Il s’agit en effet de variables propositionnelles qui représentent intuitivement des propositions élémentaires qui sont soit vraies soit fausses. Par exemple, « L'épice est une drogue » est un fait ;
  • Les clauses négatives représentent des buts à atteindre, i.e. des questions. En effet, si l’on veut prouver 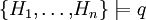\{ H_{1} \text{,} \ldots \text{,} H_{n} \} \models q, alors q est le but de la résolution. Or on peut se ramener, via le principe de déduction en appliquant une technique d’inconsistance, à 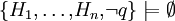\{ H_{1} \text{,} \ldots \text{,} H_{n} \text{,} \lnot q \} \models \empty. La clause 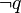\lnot q est une clause de Horn négative qui modélise bien le but à atteindre.

Applications en programmation logique

Quel est le domaine d’application des clauses de Horn ?

Les formes normales composées de clauses de Horn sont un cas particulier de formes normales pour lesquelles on connait des méthodes de résolution efficaces. En effet le problème de la satisfiabilité d’un ensemble de clauses de Horn — aussi appelé HORN–SAT — est dans la classe 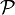\mathcal{P} et complet pour cette classe. Les clauses de Horn jouent donc un rôle fondamental en programmation logique[1].

Les formules logiques que le langage de programmation Prolog peut utiliser sont des clauses de Horn, autrement dit Prolog est entièrement basé sur des clauses de Horn. Les éléments évoqués ci–dessus ne permettent d’utiliser que des variables propositionnelles et non des prédicats. Or Prolog opère en logique du premier ordre. Il est donc nécessaire d’étendre ces résultats au calcul des prédicats.

Un autre intérêt des clauses de Horn dans la preuve de théorème par calcul des prédicats du premier ordre est que l’on peut réduire deux clauses de Horn à une clause de Horn. En preuve automatique des théorèmes, on peut atteindre une très grande efficacité en représentant les prédicats sous forme de clause[2].

Bibliographie

  • R. Cori et D. Lascar, Logique mathématique, Dunod, 2003, (ISBN 2-10005-452-X)
  • J.-M. Alliot, T. Schiex, P.Brisset et F. Garcia, Intelligence artificielle & informatique théorique, Cépaduès, 2002, (ISBN 2-85428-578-6)

Notes

  1. ↑ Il serait intéressant d’ajouter des liens vers des papiers, articles ou implémentations de HORN–SAT. On pourra se rapporter à la version anglaise de l'article HORN–SAT.
  2. ↑ Cette partie mérite aussi d’être complétée.
  • Portail de la logique Portail de la logique
Ce document provient de « Clause de Horn ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Clause de horn de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • Clause De Horn — Pour les articles homonymes, voir Horn. La dénomination « clause de Horn » vient du nom du logicien Alfred Horn qui, le premier, met en évidence l’intérêt de telles clauses en 1951 dans l’article « On sentences which are true of… …   Wikipédia en Français

  • Clause de Horn — Pour les articles homonymes, voir Horn. En logique, en particulier en calcul propositionnel, une clause de Horn est une clause comportant au plus un littéral positif. Il existe donc trois types de clauses de Horn : celles qui comportent un… …   Wikipédia en Français

  • Clause (Logique) — Pour les articles homonymes, voir Clause. Une clause en logique booléenne est une disjonction de littéraux. En calcul propositionnel, une clause est de la forme : où les li sont des littéraux. La clause vide, c est à dire la disjonction de 0 …   Wikipédia en Français

  • Horn-satisfiability — In formal logic, Horn satisfiability, or HORNSAT, is the problem of deciding whether a given set of propositional Horn clauses is satisfiable.A Horn clause is a clause with at most one positive literal, called the head of the clause, and any… …   Wikipedia

  • Clause (logique) — Pour les articles homonymes, voir Clause. Une clause en logique booléenne est une disjonction de littéraux. En calcul propositionnel, une clause est de la forme : où les li sont des littéraux. La clause vide, c est à dire la disjonction de 0 …   Wikipédia en Français

  • Horn — may refer to: * Horn (anatomy), the pointed projection of the skin of various animals, as an organ or its material * Horn (surname)In music and sound * Horn (instrument), sometimes called a French horn, a brass musical instrument constructed of… …   Wikipedia

  • Horn (surname) — Horn is a surname, and may refer to:* Alan F. Horn * Alfred Horn (1918–2001), American mathematician ** Horn clause is a term in formal logic named after him * Alfred Aloysius Trader Horn, an African trader during the Scramble for Africa * Anton… …   Wikipedia

  • Horn clause — In mathematical logic, a Horn clause is a clause (a disjunction of literals) with at most one positive literal. They are named after the logician Alfred Horn, who first pointed out the significance of such clauses in 1951. Horn clauses play a… …   Wikipedia

  • Clause (logic) — For other uses, see Clause (disambiguation). In logic, a clause is a finite disjunction of literals.[1] Clauses are usually written as follows, where the symbols li are literals: In some cases, clauses are written (or defined) as sets of literals …   Wikipedia

  • Alfred Horn — (17 février 1918 16 avril 2001) est un mathématicien américain réputé pour ses travaux dans le domaine des treillis et de l algèbre universelle. Son article intitulé « On sentences which are true of direct unions of algebras » (Journal… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”