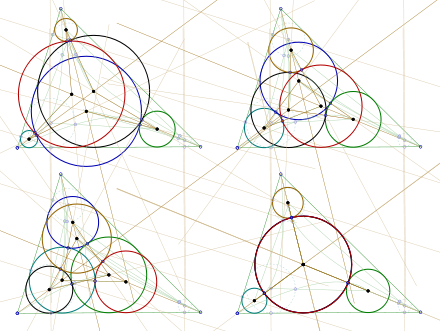
Théorème des six cercles

Théorème des six cercles
Diverses configurations illustrant le théorème. Dans la dernière, les cercles sont une fois sur deux confondus avec le cercle rouge.

En géométrie euclidienne plane, le théorème des six cercles s'énonce ainsi :

Soit un triangle vrai quelconque, les côtés étant numérotés c1, c2 c3. On considère un cercle Γ1 quelconque, tangent aux côtés c1 et c2. Puis le cercle Γ2 tangent à Γ1, c2 et c3, le cercle Γ3 tangent à Γ2, c3 et c1, et ainsi de suite en « tournant » dans le triangle. Alors, le cercle Γ6 est tangent à Γ1.

Autrement dit, le septième cercle construit est confondu avec le premier. La suite des cercles , a priori infinie, n'est, d'après le théorème, constituée que de six cercles différents.


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème des six cercles de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… …   Wikipédia en Français

  • Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants  …   Wikipédia en Français

  • Liste Des Théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Liste des theoremes — Liste des théorèmes Liste des théorèmes par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le… …   Wikipédia en Français

  • Liste des théorèmes — par ordre alphabétique. Pour l établissement de l ordre alphabétique, il a été convenu ce qui suit : Si le nom du théorème comprend des noms de mathématiciens ou de physiciens, on se base sur le premier nom propre cité. Si le nom du théorème …   Wikipédia en Français

  • Histoire Des Mathématiques — Article de la série Histoire des sciences Chronologie Chronologie des sciences Chronologie de l astronomie …   Wikipédia en Français

  • Histoire des mathematiques — Histoire des mathématiques Article de la série Histoire des sciences Chronologie Chronologie des sciences Chronologie de l astronomie …   Wikipédia en Français

  • Histoire des mathématiques — L’histoire des mathématiques s étend sur plusieurs millénaires et dans de nombreuses régions du globe allant de la Chine à l’Amérique centrale. Jusqu au XVIIe siècle, le développement des connaissances mathématiques s’effectue… …   Wikipédia en Français

  • Triangle — Pour les articles homonymes, voir Triangle (homonymie). Un triangle. En géométrie euclidienne, un trian …   Wikipédia en Français

  • Cercle Des Neuf Points — Cercle d Euler Cercle et droite d Euler d un triangle En géométrie, le cercle d Euler d un triangle (aussi appelé cercle des neuf points, cercle de Feuerbach, cercle de Terquem, cercle médian) est l unique cercle passant par les neuf points… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”