Soliton de Peregrine

Soliton de Peregrine
Vue 3D de l'évolution spatio-temporelle du soliton de Peregrine

Le soliton de Peregrine est une solution mathématique de l'équation de Schrödinger non-linéaire[1]. Cette solution a été établie en 1983 par Howell Peregrine, chercheur au département de mathématiques de l'Université de Bristol.

Sommaire

Propriétés

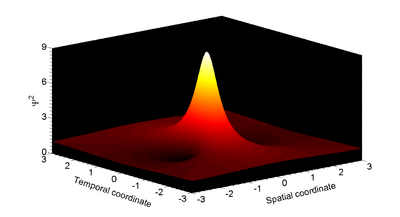
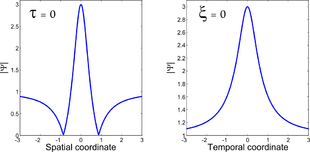
Au contraire du soliton fondamental qui a la propriété de conserver sa forme caractéristique inchangée durant sa propagation, le soliton de Peregrine présente une double localisation, à la fois dans le domaine temporel et dans le domaine spatial. Ainsi, à partir d'une petite oscillation sur un fond continu, le soliton de Peregrine se développe, voyant sa durée temporelle diminuer et son amplitude augmenter. Au point de compression maximale, son amplitude atteint trois fois l'amplitude du fond continu environnant (si l'on raisonne en intensité comme c'est le cas en optique, c'est un facteur 9 qui sépare le pic du soliton du fond environnant). Passé ce point de compression maximale, l'onde voit son amplitude diminuer et s'élargit pour finalement disparaître.

Ce comportement du soliton de Peregrine correspond aux critères habituellement retenus pour qualifier une vague scélérate. Le soliton de Peregrine représente ainsi une explication potentielle attirante de la formation de ces vagues d'une amplitude anormalement élevée qui apparaissent et disparaissent sans laisser de trace [2].

Expression mathématique

Dans le domaine spatio-temporel

Profils spatial et temporel au point de compression maximal

Le soliton de Peregrine est solution de l'équation de Schrödinger non-linéaire unidimensionnelle qui peut s'écrire sous la forme normalisée suivante :

i \frac{\partial \psi}{\partial \tau} + \frac{1}{2} \frac{\partial^2 \psi}{\partial^2 \xi} + |\psi|^2 \psi = 0

avec ξ coordonnée spatiale et τ coordonnée temporelle. ψ(ξ,τ) représentant l'enveloppe d'une onde de surface se propageant en eau profonde. La dispersion est considérée anormale et la non-linéarité autofocalisante.

Le soliton de Peregrine a pour expression dans le domaine spatio-temporel :

\psi (\xi, \tau) = \left[ 1-\frac{4 (1 + 2 i \tau)}{1+4 \xi^2 + 4 \tau^2} \right] e^{i \tau}

si bien que ses maxima temporel et spatial sont atteints en ξ = 0 et τ = 0.

Le soliton de Peregrine est un soliton rationnel d'ordre 1. Il peut également être vu comme un cas limite d'une classe de solitons à respiration appelés breathers d'Akhmediev.

Dans le domaine spectral

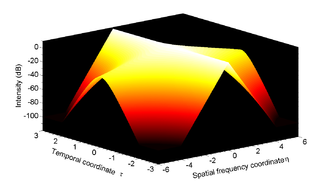Evolution du spectre du soliton de Peregrine [3]

À partir de la transformée de Fourier de ψ, il est également possible d'exprimer mathématiquement le soliton de Peregrine en fonction de la fréquence spatiale η [3]:

\tilde{\psi} (\eta, \tau) = \frac{1}{\sqrt{2 \pi}} \int{\psi (\xi, \tau) e^{i \eta \xi} d\xi} = \sqrt{2 \pi} e^{i \tau} \left[ \frac{1+2 i \tau}{\sqrt{1+4 \tau^2}} exp \left( -\frac{|\eta|}{2} \sqrt{1+4 \tau^2} \right) - \delta(\eta) \right]

avec δ étant la distribution de Dirac.

Cela correspond à un module (avec le fond continu correspondant à la distribution de Dirac omis) : |\tilde{\psi} (\eta, \tau)| = \sqrt{2 \pi} exp \left( -\frac{|\eta|}{2} \sqrt{1+4 \tau^2} \right)

De manière intéressante, il est possible de remarquer qu'à n'importe quel instant fixé τ, si le module du spectre est représenté en échelle logarithmique, il aura alors une forme triangulaire caractéristique avec une pente étant en valeur absolue \frac{\sqrt{1+4 \tau^2}}{2}. Le spectre est donc le plus étendu (i.e. la décroissance du spectre est la plus faible) en \tau = 0. Cela correspond sans surprise au point de compression maximale.

Démonstrations expérimentales

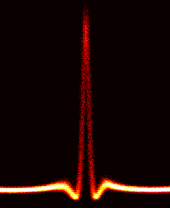Enregistrement du profil temporel d'un soliton de Peregrine en optique [4]

Les prédictions mathématiques de H. Peregrine ont été initialement établies dans le domaine hydrodynamique. C'est pourtant dans un tout autre domaine que le soliton de Peregrine a pu être pour la première fois démontré expérimentalement et caractérisé.

En 2010, soit plus de 25 ans après les travaux de Peregrine, des chercheurs ont exploité l'analogie qui peut être dressée entre le monde de l'hydrodynamique et l'optique pour générer dans des fibres optiques des solitons de Peregrine [5],[6]. En effet, la propagation d'une impulsion dans une fibre optique et l'évolution d'une vague en eau profonde répondent toutes les deux à l'équation de Schrödinger non-linéaire (moyennant néanmoins une inversion des variables de temps et d'espace). Une telle analogie avait déjà été exploitée par le passé pour générer dans les fibres optiques des solitons optiques. De manière intéressante et en se basant uniquement sur des composants des télécommunications optiques , il a été montré qu'avec même une condition initiale approchée (dans leur cas, une modulation initiale sinusoidale), un profil très proche du soliton de Peregrine pouvait être généré [4],[7]. Le profil spectral triangulaire typique a également été confirmé expérimentalement [4],[5],[8].


Ces résultats en optique ont été confirmés dès 2011 dans le domaine hydrodynamique[9],[10] par des expériences menées dans un canal d'une quinzaine de mètres de long. D'autres expériences menées dans de domaine de la physique des plasmas également régie par l'équation de Schrödinger non-linéaire ont également montré l'universalité de cette forme d'onde [11].

Notes et références

  1. ↑ D. H. Peregrine, « Water waves, nonlinear Schrödinger equations and their solutions », dans J. Austral. Math. Soc. Ser. B, vol. 25, 1983, p. 16-43 [lien DOI] 
  2. ↑ V.I. Shrira, « What makes the Peregrine soliton so special as a prototype of freak waves ? », dans J. Eng. Math., 2009 
  3. ↑ a et b Akhmediev, N., Ankiewicz, A. , Soto-Crespo, J. M. and Dudley J. M., « Universal triangular spectra in parametrically-driven systems », dans Phys. Lett. A, vol. 375, 2011, p. 775-779 
  4. ↑ a, b et c K. Hammani, « Peregrine soliton generation and breakup in standard telecommunications fiber », dans Optics Letters, vol. 36, 2011, p. 112-114 [lien DOI] 
  5. ↑ a et b B. Kibler, « The Peregrine soliton in nonlinear fibre optics », dans Nature Physics, 2010 [lien DOI] 
  6. ↑ Peregrine’s 'Soliton' observed at last, bris.ac.uk. Consulté le 2010-08-24
  7. ↑ M. Erkintalo, « Akhmediev breather evolution in optical fiber for realistic initial conditions », dans Phys. Lett. A, vol. 375, 2011, p. 2029-2034 
  8. ↑ Hammani K., Wetzel B. , Kibler B. , Fatome J., Finot C. , Millot G., Akhmediev N., and Dudley J. M., « Spectral dynamics of modulation instability described using Akhmediev breather theory », dans Opt. Lett., vol. 36, no 2140-2142, 2011 [lien DOI] 
  9. ↑ A. Chabchoub, « Rogue wave observation in a water wave tank », dans Phys. Rev. Lett., 2011 [lien DOI] 
  10. ↑ Rogue waves captured, www.sciencenews.org. Consulté le 2011-06-03
  11. ↑ H. Bailung, « Observation of Peregrine solitons in a multicomponent plasma with negative ions », dans Phys. Rev. Lett., 2011 


Sur les autres projets Wikimedia :


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Soliton de Peregrine de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Soliton optique — fondamental Un soliton optique est une impulsion électromagnétique se propageant sans déformation. Par sa nature même, elle est solution stable de l équation de propagation dans le milieu qu elle traverse (typiquement une fibre optique). Sommaire …   Wikipédia en Français

  • Soliton — Un soliton est une onde solitaire qui se propage sans se déformer dans un milieu non linéaire et dispersif. On en trouve dans de nombreux phénomènes physiques de même qu ils sont la solution de nombreuses équations aux dérivées partielles non… …   Wikipédia en Français

  • Howell Peregrine — D. Howell Peregrine Naissance 30 Décembre 1938 Décès 20 Mars 2007 Bristol (Royaume Uni) Champs Mécanique des fluides Institution Université de Bristol Diplômé de Université d Oxford Université de Cambridge …   Wikipédia en Français

  • Vague scélérate — vue d’un navire marchand (1940, Golfe de Gascogne, ligne de sonde des 100 brasses). Les vagues scélérates sont des vagues océaniques très hautes, soudaines, qui étaient considérées comme très rares, même si aujourd’hui on sait qu’elles… …   Wikipédia en Français

  • Rogue wave — This article is about the deep ocean rogue waves which occur far out at sea. For tsunami and tidal wave phenomena, see those respective articles. For other uses, see Rogue wave (disambiguation). The Draupner wave, a single giant wave measured on… …   Wikipedia

  • Breather — A breather is a nonlinear wave in which energy concentrates in a localized and oscillatory fashion. This contradicts with the expectations derived from the corresponding linear system for infinitesimal amplitudes, which tends towards an even… …   Wikipedia

  • Boussinesq approximation (water waves) — In fluid dynamics, the Boussinesq approximation for water waves is an approximation valid for weakly non linear and fairly long waves. The approximation is named after Joseph Boussinesq, who first derived them in response to the observation by… …   Wikipedia

  • Волны-убийцы — Фотография большой волны, надвигающейся на торговое судно. Приблизительно 1940 е годы Волны убийцы (Блуждающие волны, волны монстры, белая волна, англ. rogue wave  в …   Википедия

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”