Méthode de Fizeau
- Méthode de Fizeau
-
La méthode de Fizeau est un moyen de mesurer la distance angulaire entre deux étoiles grâce à un interferomètre de Young.
Comme toutes les expériences faisant intervenir les interférences, elle fait appel à l'aspect ondulatoire de la lumière.
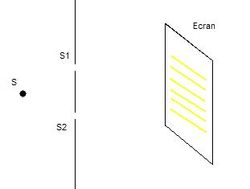
Schéma de principe des fentes de Young.
Ici, on a deux sources lumineuses, les deux étoiles, qui ne sont pas cohérentes entre elles. L'absence de cohérence implique qu'il ne pourra pas y avoir d'interférences entre la lumière émise par l'une et la lumière émise par l'autre.
Pour simplifier, on placera l'étoile 1 sur l'axe optique (l'axe de symétrie du système) et l'on mesurera la distance entre le centre des figures d'interférences de l'étoile 1 (ici l'axe optique) et le centre des figures d'interférences de l'étoile 2. On peut ainsi acceder à l'écart angulaire (et éventuellement la distance) entre les étoiles par la position entre ces deux centres.
Articles connexes
Un brin d'astronomie par Yaël Nazé
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Méthode de Fizeau de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Fizeau — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Patronyme Hippolyte Fizeau (1819 1896), physicien et astronome français, qui donna son nom à : l effet Doppler Fizeau, l appareil de Fizeau, l… … Wikipédia en Français
FIZEAU (A. H. L.) — FIZEAU ARMAND HIPPOLYTE LOUIS (1819 1896) Physicien français, né à Paris et mort au château de Venteuil, près de La Ferté sous Jouarre (Seine et Marne). Professeur à l’École polytechnique (1863), Fizeau est le premier à mesurer la vitesse de la… … Encyclopédie Universelle
Fizeau — (spr. fisō), Armand Hippolyte Louis, Physiker, geb. 23. Sept. 1819 in Paris, gest. 18. Sept. 1896 in Venteuil (Seine et Marne), lebte in Paris als Privatmann, wurde 1860 Mitglied der Akademie und 1878 des Längenbureaus. Er arbeitete über die… … Meyers Großes Konversations-Lexikon
Fizeau — Hippolyte Fizeau. Armand Hippolyte Louis Fizeau (* 23. September 1819 in Paris; † 18. September 1896 in Venteuil bei Épernay) war ein französischer Physiker. Fizeau beschäftigte sich als Privatgelehrter mit Physik und Astronomie. 1860 wurde er in … Deutsch Wikipedia
Méthode des vitesses radiales — Diagramme montrant l influence d un petit objet (comme une planète) orbitant autour d un autre, beaucoup plus massif (comme une étoile). Le petit corps produit en effet des changements de vélocité sur le plus grand, de telle sorte que les deux… … Wikipédia en Français
méthode sur le principe de Fizeau — interferometrinis metodas statusas T sritis Standartizacija ir metrologija apibrėžtis Netiesioginis dangos storio matavimas, kai laiptelio aukštis matuojamas interferometru. atitikmenys: angl. Fizeau multiple beam interferometry method vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Fizeau multiple-beam interferometry method — interferometrinis metodas statusas T sritis Standartizacija ir metrologija apibrėžtis Netiesioginis dangos storio matavimas, kai laiptelio aukštis matuojamas interferometru. atitikmenys: angl. Fizeau multiple beam interferometry method vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Expérience de Fizeau — Schéma de l expérience de Fizeau. L est la lumière, S1 le 1er miroir, Z la roue dentée, S2 le 2e miroir et B l observateur. L expérience de Fizeau est une expérience destinée à mesurer la vitesse de la lumière. Réalisée pour la première fois en… … Wikipédia en Français
Hippolyte Fizeau — Naissance 23 septembre 1819 Paris (France) Décès 18 septembre 1896 (à 76 ans) … Wikipédia en Français
Armand Fizeau — Hippolyte Fizeau. Armand Hippolyte Louis Fizeau (* 23. September 1819 in Paris; † 18. September 1896 in Venteuil bei Épernay) war ein französischer Physiker. Fizeau beschäftigte sich als Privatgelehrter mit Physik und Astronomie. 1860 wurde er in … Deutsch Wikipedia

