Suite de Conway

La suite de Conway est une suite mathématique inventée en 1986 par le mathématicien John Horton Conway, initialement sous le nom de « suite audioactive »^[1]. Elle est également connue sous le nom anglais de Look and Say (« regarder et dire »). Dans cette suite, un terme se détermine en annonçant les chiffres formant le terme précédent.

Définition

Suite de Conway

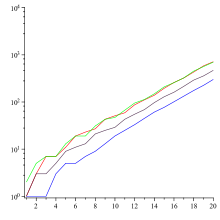Graphe représentant, en ordonnées, le nombre de chiffres du n^e terme de la suite de Conway, avec n en abscisses, dans un repère semi-logarithmique. Chaque courbe correspond à un terme initial différent : 1 (bleu), 23 (rouge), 13 (violet), 312 (vert). Les courbes tendent vers une droite dont la pente correspond à la constante de Conway.

Le premier terme de la suite de Conway est posé comme égal à 1. Chaque terme de la suite se construit en annonçant le terme précédent, c'est-à-dire en indiquant combien de fois chacun de ses chiffres se répète.

Concrètement :

X₀ = 1

Ce terme comporte juste un « 1 ». Par conséquent, le terme suivant est :

X₁ = 11

Celui-ci est composé de deux « 1 » :

X₂ = 21

En poursuivant le procédé :

X₃ = 1211

X₄ = 111221

X₅ = 312211

X₆ = 13112221

Et ainsi de suite.

Il est possible de généraliser le procédé en prenant un terme initial différent de 1. Dans le reste de l'article, on supposera que ce n'est pas le cas.

Les 20 premiers termes

Terme 1 = 1

Terme 2 = 11

Terme 3 = 21

Terme 4 = 1211

Terme 5 = 111221

Terme 6 = 312211

Terme 7 = 13112221

Terme 8 = 1113213211

Terme 9 = 31131211131221

Terme 10 = 13211311123113112211

Terme 11 = 11131221133112132113212221

Terme 12 = 3113112221232112111312211312113211

Terme 13 = 1321132132111213122112311311222113111221131221

Terme 14 = 11131221131211131231121113112221121321132132211331222113112211

Terme 15 = 311311222113111231131112132112311321322112111312211312111322212311322113212221

Terme 16 = 132113213221133112132113311211131221121321131211132221123113112221131112311332111213211322211312113211

Terme 17 = 11131221131211132221232112111312212321123113112221121113122113111231133221121321132132211331121321231231121113122113322113111221131221

Terme 18 = 31131122211311123113321112131221123113112211121312211213211321322112311311222113311213212322211211131221131211132221232112111312111213111213211231131122212322211331222113112211

Terme 19 = 1321132132211331121321231231121113112221121321132122311211131122211211131221131211132221121321132132212321121113121112133221123113112221131112311332111213122112311311123112111331121113122112132113213211121332212311322113212221

Terme 20 = 11131221131211132221232112111312111213111213211231132132211211131221131211221321123113213221123113112221131112311332211211131221131211132211121312211231131112311211232221121321132132211331121321231231121113112221121321133112132112312321123113112221121113122113121113123112112322111213211322211312113211

Propriétés

Les principales propriétés de cette suite sont :

• Aucun terme de la suite ne comporte un chiffre supérieur à 3.
• Tous les termes de la suite possèdent un nombre pair de chiffres, sauf le terme initial.
• Les termes de rang impair se terminent par 11 et les termes de rang pair par 21 (là encore à l'exception du terme initial).
• En moyenne, les termes de la suite possèdent 50 % de chiffres 1, 31 % de 2 et 19 % de 3.
• Le nombre L_n de chiffres du n^e terme de la suite est équivalent à Cλⁿ, où est un nombre algébrique de degré 71 nommé constante de Conway, et C est une autre constante. En particulier :

  

Ces propriétés restent vraies dans le cas général où le premier terme de la suite est choisi différent de 1 (et de 22, puisque dans ce cas la suite est constante), avec une constante C qui dépend de ce choix, mais avec toujours la même constante λ.

Racines du polynôme de Conway sur le plan complexe.

La constante de Conway est l'unique solution réelle positive de l'équation polynomiale suivante :

x⁷¹ − x⁶⁹ − 2x⁶⁸ − x⁶⁷ + 2x⁶⁶ + 2x⁶⁵ + x⁶⁴ − x⁶³ − x⁶² − x⁶¹ − x⁶⁰ − x⁵⁹ +

2x⁵⁸ + 5x⁵⁷ + 3x⁵⁶ − 2x⁵⁵ − 10x⁵⁴ − 3x⁵³ − 2x⁵² + 6x⁵¹ + 6x⁵⁰ + x⁴⁹ + 9x⁴⁸ − 3x⁴⁷ −

7x⁴⁶ − 8x⁴⁵ − 8x⁴⁴ + 10x⁴³ + 6x⁴² + 8x⁴¹ − 5x⁴⁰ − 12x³⁹ + 7x³⁸ − 7x³⁷ + 7x³⁶ + x³⁵ −

3x³⁴ + 10x³³ + x³² − 6x³¹ − 2x³⁰ − 10x²⁹ − 3x²⁸ + 2x²⁷ + 9x²⁶ − 3x²⁵ + 14x²⁴ − 8x²³ −

7x²¹ + 9x²⁰ + 3x¹⁹ − 4x¹⁸ − 10x¹⁷ − 7x¹⁶ + 12x¹⁵ + 7x¹⁴ + 2x¹³ − 12x¹² − 4x¹¹ −

2x¹⁰ + 5x⁹ + x⁷ − 7x⁶ + 7x⁵ − 4x⁴ + 12x³ − 6x² + 3x − 6 = 0

On a l'approximation

« Désintégration audioactive »

John Conway qualifia initialement cette suite de « désintégration audioactive » (audioactive decay en anglais), un jeu de mots sur la désintégration radioactive, en remarquant le comportement des différents termes de la suite.

Il montra qu'à partir d'un certain point, presque tous les termes de la suite peuvent être décomposés en 92 sous-termes (nommés éléments, par analogie avec les éléments chimiques) qui se décomposent au terme suivant en un certain nombre d'autres éléments.

Par exemple, l'élément le plus simple, nommé hydrogène, est la séquence 22 qui donne elle-même au terme suivant. La séquence 3113322112 est dénommée manganèse ; au terme suivant, elle donne 132123222112 qui se décompose en les séquences prométhium (132) et sodium (123222112).

Il a été montré que si l'on débute la suite par le terme uranium 3, les 91 autres éléments seront apparus dans un terme ou un autre au bout de 91 itérations. Cette suite porte d'ailleurs en anglais le nom de Conway's sequence.

Algorithme (python)

def TermeSuivant (valeurstr):

  nouveauterme=""
  a=0
  while(a<len(valeurstr)):
      nb=1
      if(a+1>=len(valeurstr)):
          nouveauterme=nouveauterme+"1"+valeurstr[a]
          a=a+1
      elif(valeurstr[a]!=valeurstr[a+1]):
          nouveauterme=nouveauterme+"1"+valeurstr[a]
          a=a+1           
      else:
          while (a+2<=len(valeurstr) and valeurstr[a]==valeurstr[a+1]):
              nb=nb+1
              a=a+1
          nouveauterme=nouveauterme+str(nb)+valeurstr[a]
          a=a+1
  return nouveauterme

while(1):

  rangmax=int(input("Jusqu'à quel rang ? ")) # On demande le rang maximal
  rang=1
  valeurstr="1"
  print("Terme",rang,"=",valeurstr)
  while(rang<rangmax):
      rang=rang+1
      print("Terme",rang,"=",TermeSuivant(valeurstr))
      valeurstr=TermeSuivant(valeurstr)
  print("\n")

Références

Annexes

Articles connexes

• Suite de Robinson
• Run-length encoding
• Suite (mathématiques)

Liens externes

• (en) Suite A005150 sur l'Encyclopédie en ligne des suites de nombres entiers
• (en) Eric W. Weisstein, « Look and Says Sequence », sur MathWorld
• (en) Henry Bottomley, « Evolution of Conway's 92 Look and Say audioactive elements » : une compilation des 92 éléments « audioactifs » de la suite

• Portail des mathématiques