- Règle de golomb
-
Règle de Golomb
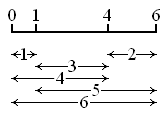Règle de Golomb d'ordre 4 et de longueur 6. Cette règle est optimale et parfaite.En mathématiques, une règle de Golomb, appelée ainsi en l'honneur du mathématicien Solomon W. Golomb, est une règle munie de marques à des positions entières, telle que deux paires de marques ne soient jamais à la même distance ; en d'autres termes, chaque couple de marques mesure une longueur différente des autres. Puisque n'importe quelle « translation entière » d'une règle de Golomb donne une règle de Golomb, la première marque est généralement portée sur 0.
Par définition, l'ordre d'une règle de Golomb est le nombre de marques qu'elle porte ; la longueur d'une règle de Golomb est la plus grande distance entre deux de ses marques.
Il n'est pas nécessaire qu'une règle de Golomb permette de mesurer toutes les distances entre 0 et la longueur de la règle mais si c'est le cas, on dit qu'il s'agit d'une règle de Golomb parfaite.
La plus courte règle de Golomb pour un ordre donné s'appelle une règle de Golomb optimale. Construire une règle de Golomb n'est pas difficile mais trouver toutes les règles de Golomb d'un ordre donné est un défi informatique (voir distributed.net, un projet de calcul distribué actuellement en cours pour trouver des règles de Golomb optimales).
Une des applications pratiques des règles de Golomb est la conception d'« antenne réseau à commande de phase » comme dans les radiotélescopes. L'application la plus courante de la règle de Golomb aux antennes est la répartition des antennes des réseaux cellulaires.
Sommaire
Exemples de règles de Golomb
- [0,1,3] (optimale)
- [0,1,3,7] (pas optimale)
- [0,1,4,6] (optimale)
- [1,2,4,8,16,...,2n,...] (pas optimale)
Règles de Golomb optimales
Ordre Longueur Marques 1 0 0 2 1 0 1 3 3 0 1 3 4 6 0 1 4 6
0 2 5 65 11 0 1 4 9 11
0 2 7 8 116 17 0 1 4 10 12 17
0 1 4 10 15 17
0 1 8 11 13 17
0 1 8 12 14 177 25 0 1 4 10 18 23 25
0 1 7 11 20 23 25
0 1 11 16 19 23 25
0 2 3 10 16 21 25
0 2 7 13 21 22 258 34 0 1 4 9 15 22 32 34 9 44 0 1 5 12 25 27 35 41 44 10 55 0 1 6 10 23 26 34 41 53 55
0 2 14 21 29 32 45 49 54 5511 72 0 1 4 13 28 33 47 54 64 70 72
0 1 9 19 24 31 52 56 58 69 72
0 2 8 18 25 39 44 59 68 71 72
0 3 14 16 20 41 48 53 63 71 7212 85 0 2 6 24 29 40 43 55 68 75 76 85 13 106 0 2 5 25 37 43 59 70 85 89 98 99 106 14 127 0 4 6 20 35 52 59 77 78 86 89 99 122 127 15 151 0 4 20 30 57 59 62 76 100 111 123 136 144 145 151 16 177 0 1 4 11 26 32 56 68 76 115 117 134 150 163 168 177 17 199 0 5 7 17 52 56 67 80 81 100 122 138 159 165 168 191 199 18 216 0 2 10 22 53 56 82 83 89 98 130 148 153 167 188 192 205 216 19 246 0 1 6 25 32 72 100 108 120 130 153 169 187 190 204 231 233 242 246 20 283 0 1 8 11 68 77 94 116 121 156 158 179 194 208 212 228 240 253 259 283 21 333 0 2 24 56 77 82 83 95 129 144 179 186 195 255 265 285 293 296 310 329 333 22 356 0 1 9 14 43 70 106 122 124 128 159 179 204 223 253 263 270 291 330 341 353 356 23 372 0 3 7 17 61 66 91 99 114 159 171 199 200 226 235 246 277 316 329 348 350 366 372 24 425 0 9 33 37 38 97 122 129 140 142 152 191 205 208 252 278 286 326 332 353 368 384 403 425 25 480 0 12 29 39 72 91 146 157 160 161 166 191 207 214 258 290 316 354 372 394 396 431 459 467 480 26 492 0 1 33 83 104 110 124 163 185 200 203 249 251 258 314 318 343 356 386 430 440 456 464 475 487 492 Le 24 février 2009, le projet de calcul partagé distributed.net a annoncé avoir découvert la règle de Golomb optimale pour l'ordre 26.
Références
- Martin Gardner, « Mathematical games », Scientific American, Mai 1972, p. 108-112
Lien externe
- (fr) Site du projet distributed.net: Page sur les règles de Golomb
Portail des mathématiques
Catégorie : Instrument de géométrie
Wikimedia Foundation. 2010.
