Relations de reciprocité d'Onsager

Relations de reciprocité d'Onsager

Relations de réciprocité d'Onsager

En thermodynamique des systèmes hors équilibre, les relations de réciprocité d'Onsager relient des quantités nommées flux et forces dans le cadre de systèmes hors de l'équilibre global, mais suffisamment proche de celui-ci pour être régis par une certaine forme d'équilibre local :

  • Par exemple, on remarque que les différences de température dans un système entrainent des flux de chaleur des parties chaudes vers les parties froides du système.
  • De même, les différences de pression entrainent des flux de matière des zones où la pression est importante vers celles où elle l'est moins.
  • Il a été observé expérimentalement que quant à la fois la pression et la température varient, les différences de pression peuvent provoquer des modifications des flux de chaleurs et de la température. De façon encore plus surprenante, le flux de chaleur par unité d'écart de pression et le flux de densité (de matière) par unité de température sont égaux. Ceci a été démontré par Lars Onsager dans le cadre de la physique statistique hors d'équilibre.

Des relations de réciprocité similaires adviennent entre les différentes paires de forces et de flux dans de nombreux systèmes physiques. La théorie développée par Onsager est bien plus générale que cet exemple et est capable de traiter plus de deux forces thermodynamiques à la fois.

Sommaire

Exemple: système de fluides

Potentiels thermodynamiques, forces et flux

Le potentiel thermodynamique fondamental est l'énergie interne. Dans un système fluide, u dépend de la densité de matière r et de la densité d'entropie s de la façon suivante

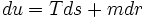
du=Tds+mdr ~

ou Test la température et m une combinaison de la pression et du potentiel chimique. Nous pouvons écrire:

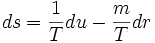
ds={1\over T}du-{m\over T}dr

les quantités extensives u et r sont conservées et leurs flux satisfont aux equations de continuité:

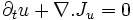
\partial_t u+\nabla . J_u=0


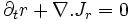
\partial_t r+\nabla . J_r=0


ou 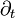\partial_t indique la derivée partielle par rapport à la variable t et \nabla . la divergence du flux de densité J. Les gradients des variables conjuguées de u et de r , qui sont 1/T et -m/T sont des forces thermodynamiques et elles provoquent l'apparition de flux des variables extensives correspondantes. En l'absence de flux de matière, nous avons:

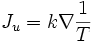
J_u=k\nabla {1\over T}


et en l'absence de flux de chaleur:

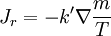
J_r=-k'\nabla {m\over T}


ou \nabla signifie maintenant le gradient.

Les relations de réciprocité

Dans cet exemple où on trouve à la fois des flux de chaleur et de matière, il y a des termes croisés dans la relation entre forces et flux (les coefficients de proprortionalité étant habituellement notés L)

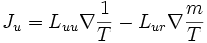
J_u=L_{uu} \nabla {1\over T}-L_{ur} \nabla {m\over T}


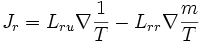
J_r=L_{ru} \nabla {1\over T}-L_{rr} \nabla {m\over T}


La relation de réciprocité de Onsager établit l'égalité de Lur et Lru. La proportionnalité découle d'une simple analyse dimensionelle. La relation d'Onsager se démontre par une étude des fluctuations thermodynamiques autour de l'état d'équilibre (voir les références).

Formulation abstraite

Soit Ei un jeu de variables extensives dont dépend une entropie S. Dans l'analyse suivante, ces symboles réfereront à la densité de ces quantités thermodynamiques. Alors

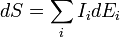
\ dS=\sum_{i}I_{i}dE_{i}

ou

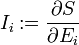
I_{i} :=\frac{\partial{S}}{\partial{E_{i}}} \!

définit les quantités intensives Ii conjuguées des quantités extensives Ei. Les gradients des quantités intensives sont les forces thermodynamiques:

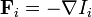
\mathbf{F}_{i} = -\nabla{I_{i}} \!

et elles gouvernent les flux Ji par les equations de continuité:

\partial_{t}E_{i} + \nabla \cdot \mathbf{J}_{i} = 0 \!

Les flux sont proportinonnels aux forces thermodynamiques par les coefficients d'une matrice Lij

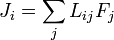
\ J_{i}=\sum_{j}L_{ij}F_{j}

alors

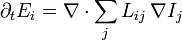
\partial_{t}E_{i} = \nabla \cdot \sum_{j} L_{ij}\, \nabla{I_{j}} \!

en introduisant la matrice (σi,j)

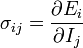
\sigma_{ij} = \frac{\partial{E_{i}}}{\partial{I_{j}}} \!

nous avons

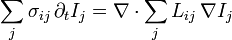
\sum_{j} \sigma_{ij}\, \partial_{t}I_{j} = \nabla \cdot \sum_{j} L_{ij}\, \nabla{I_{j}} \!

Voir aussi

Références

  1. L. D. Landau et E. M. Lifshitz, Cours de Physique Théorique, t. 5, Physique Statistique (Mir)
  2. H. Callen, Theromdynamics (Mc Graw Hill)
  3. S.R. de Groot et W. Mazur Non Equilibrium Thermodynamics (Dover)
  • Portail de la physique Portail de la physique
Ce document provient de « Relations de r%C3%A9ciprocit%C3%A9 d%27Onsager ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Relations de reciprocité d'Onsager de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Relations de reciprocite d'Onsager — Relations de réciprocité d Onsager En thermodynamique des systèmes hors équilibre, les relations de réciprocité d Onsager relient des quantités nommées flux et forces dans le cadre de systèmes hors de l équilibre global, mais suffisamment proche… …   Wikipédia en Français

  • Relations de réciprocité d'onsager — En thermodynamique des systèmes hors équilibre, les relations de réciprocité d Onsager relient des quantités nommées flux et forces dans le cadre de systèmes hors de l équilibre global, mais suffisamment proche de celui ci pour être régis par une …   Wikipédia en Français

  • Relations de réciprocité d'Onsager — En thermodynamique des systèmes hors équilibre, les relations de réciprocité d Onsager relient des quantités nommées flux et forces dans le cadre de systèmes hors de l équilibre global, mais suffisamment proche de celui ci pour être régis par une …   Wikipédia en Français

  • Relation de réciprocité d'Onsager — Théorie d Onsager La théorie d Onsager a été élaborée en 1931 par Lars Onsager. C est une théorie macroscopique du couplage linéaire de phénomènes irréversibles comme la conduction électrique et la diffusion thermique. Cette théorie émet l… …   Wikipédia en Français

  • Onsager — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Lars Onsager, physicien ; Théorie d Onsager ; Relations de réciprocité d Onsager. Catégorie : Homonymie …   Wikipédia en Français

  • ONSAGER (L.) — ONSAGER LARS (1903 1976) Chimiste et physicien américain né à Oslo de parents norvégiens. Dès 1925, Lars Onsager obtient dans cette ville son diplôme d’ingénieur chimiste à l’École technique supérieure de Norvège. Au cours de ses études, Lars… …   Encyclopédie Universelle

  • Lars Onsager — Lauréats des prix Nobel de 1968 : Lars Onsager est en deuxième position à droite Lars Onsager (27  novembre  1903 à Oslo, Norvège 5  octobre  1976 à Coral Gables, Floride, Éta …   Wikipédia en Français

  • Theorie d'Onsager — Théorie d Onsager La théorie d Onsager a été élaborée en 1931 par Lars Onsager. C est une théorie macroscopique du couplage linéaire de phénomènes irréversibles comme la conduction électrique et la diffusion thermique. Cette théorie émet l… …   Wikipédia en Français

  • Théorie d'Onsager — La théorie d Onsager a été élaborée en 1931 par Lars Onsager. C est une théorie macroscopique du couplage linéaire de phénomènes irréversibles comme la conduction électrique et la diffusion thermique. Cette théorie émet l hypothèse qu il existe… …   Wikipédia en Français

  • THERMODYNAMIQUE - Processus irréversibles linéaires — Jusqu’à ce que la thermodynamique ait été en mesure d’en fournir une présentation unifiée, les phénomènes de transport qui intéressent les milieux matériels furent étudiés de manière séparée et en ordre plutôt dispersé, sans qu’au delà… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”