Rayon de Larmor

Rayon de Larmor

Le rayon de Larmor est un concept physique permettant de décrire le mouvement d'une particule chargée soumise à un champ magnétique constant. En effet, cette particule acquiert un mouvement circulaire caractérisé par son rayon.
L'expression de ce rayon dépend de la charge de la particule Z\times e, de sa masse au repos m0, de son énergie cinétique T, et de la valeur B du champ magnétique.

En mécanique classique

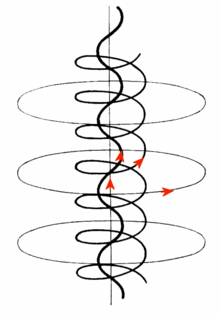Trajectoire d'une particule chargée le long d'une ligne de champ (ligne verticale). Plus la masse de la particule est importante et plus la charge est faible, plus le rayon de Larmor est grand. Si la masse est nulle, la particule suit la ligne de champ. Plus le champ est fort et plus le rayon de Larmor est petit.

Le rayon de Larmor en mécanique classique s'écrit :

R=\frac{\sqrt{2m_0T}}{ZeB}.
Démonstration :

Pour étudier le rayon de Larmor, nous nous placons dans un repère d'axes \vec{u_x}, \vec{u_y} et \vec{u_z}. Pour simplifier, supposons que le champ magnétique soit orienté selon l'axe \vec{u_z}, et que la vitesse initiale soit \vec{v_0}=v_0\vec{u_x}.
La force de Lorentz appliquée à la particule, d'expression \vec F = q \vec v \wedge \vec B, est alors contenue dans le plan \vec{u_x},\vec{u_y}. Ainsi le mouvement sera restreint à ce plan. Nous utiliserons donc uniquement les coordonnées x et y de la particule.
En appliquant le principe fondamental de la dynamique, on en déduit que ces coordonnées vérifient les équations :

m_0\ddot x+ZeB\dot y=0
et m_0\ddot y-ZeB\dot x=0.

En posant X = x + iy et Y = x − iy et ω0 = ZeB / m0, on obtient :

\ddot X-i\omega_0\dot X=0
et \ddot Y+i\omega_0\dot Y=0

Ces équations différentielles ont pour solution :

\dot x=v_0 cos(\omega_0t)
et \dot y=v_0 sin(\omega_0t)

Et en intégrant encore une fois :

x=\frac{v_0}{\omega_0} sin(\omega_0t)
et y=-\frac{v_0}{\omega_0} cos(\omega_0t)

Cela correspond à un mouvement circulaire de rayon \frac{v_0}{\omega_0}=\frac{\sqrt{2m_0T}}{ZeB}

En mécanique relativiste

Le passage en mécanique relativiste fait intervenir la grandeur \gamma=\left( 1-\frac{v^2}{c^2} \right)^{-\frac{1}{2}} (le facteur de Lorentz). En effet, il faut remplacer, dans l'expression du principe fondamental de la dynamique, la masse au repos m0 par la masse effective m = γm0. En reprenant la démonstration dans le cas classique, il faut préciser que la vitesse (ou bien \dot X \dot Y) est constante au cours du mouvement. Ainsi, γ est aussi constant, et on peut reprendre le résultat R=\frac{v_0}{\omega}=\frac{\gamma m_0 v_0}{ZeB}. Finalement, comme la mécanique relativiste nous apprend que T = (γ − 1)m0c2, on obtient la formule :

R=\frac{m_0c}{ZeB}\sqrt{\left( \frac{T+m_0c^2}{m_0c^2} \right) ^2-1}.

Remarque :

Pour retrouver la formule classique, il suffit de considérer l'énergie cinétique comme petite par rapport à l'énergie de masse au repos. On peut alors développer au premier ordre l'argument entre parenthèses sous la racine carrée.

Voir aussi


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Rayon de Larmor de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Rayon De Larmor — Le rayon de Larmor est un concept physique permettant de décrire le mouvement d une particule chargée soumise à un champ magnétique constant. En effet, cette particule acquiert un mouvement circulaire caractérisé par son rayon. L expression de ce …   Wikipédia en Français

  • Rayon de larmor — Le rayon de Larmor est un concept physique permettant de décrire le mouvement d une particule chargée soumise à un champ magnétique constant. En effet, cette particule acquiert un mouvement circulaire caractérisé par son rayon. L expression de ce …   Wikipédia en Français

  • rayon de Larmor — Larmoro spindulys statusas T sritis fizika atitikmenys: angl. Larmor radius vok. Larmor Radius, m; Larmorscher Radius, m rus. ларморов радиус, m; ларморовский радиус, m pranc. rayon de Larmor, m …   Fizikos terminų žodynas

  • Larmor radius — Larmoro spindulys statusas T sritis fizika atitikmenys: angl. Larmor radius vok. Larmor Radius, m; Larmorscher Radius, m rus. ларморов радиус, m; ларморовский радиус, m pranc. rayon de Larmor, m …   Fizikos terminų žodynas

  • Larmor-Radius — Larmoro spindulys statusas T sritis fizika atitikmenys: angl. Larmor radius vok. Larmor Radius, m; Larmorscher Radius, m rus. ларморов радиус, m; ларморовский радиус, m pranc. rayon de Larmor, m …   Fizikos terminų žodynas

  • J. Larmor — Joseph Larmor Joseph Larmor Sommaire 1 Biographie 2 Récompenses …   Wikipédia en Français

  • Joseph Larmor — Sommaire 1 Biographie 2 Récompenses …   Wikipédia en Français

  • Précession de Larmor — En physique, la précession de Larmor (nommée d après Joseph Larmor) est la précession du moment magnétique des électrons, des noyaux atomiques ou des atomes soumis à un champ magnétique. Le champ magnétique exerce un couple sur le mome …   Wikipédia en Français

  • Électron — Traduction à relire Electron → …   Wikipédia en Français

  • Larmoro spindulys — statusas T sritis fizika atitikmenys: angl. Larmor radius vok. Larmor Radius, m; Larmorscher Radius, m rus. ларморов радиус, m; ларморовский радиус, m pranc. rayon de Larmor, m …   Fizikos terminų žodynas

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”