Points de brocard
- Points de brocard
-
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Points de brocard de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Points de Brocard — En géométrie, le premier point de Brocard d un triangle ABC est le point Ω tels que les angles et orientés positivement soient égaux. Le second point de Brocard du triangle est le point Ω tels que les angles … Wikipédia en Français
Brocard-Punkte — sind spezielle Punkte im Dreieck; benannt nach dem französischen Mathematiker Henri Brocard (1845−1922). Brocard wurde am bekanntesten für den folgenden Satz: Konstruktion eines Brocard Punkts In einem Dreieck ΔABC mit den Seiten a,b,c gibt es… … Deutsch Wikipedia
Brocard — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Brocard », sur le Wiktionnaire (dictionnaire universel) Brocard est un mot français qui a plusieurs… … Wikipédia en Français
Brocard points — are special points within a triangle. They are named after Henri Brocard (1845 ndash; 1922), a French mathematician. DefinitionIn a triangle ABC with sides a , b , and c , where the vertices are labeled A , B and C in counterclockwise order,… … Wikipedia
Brocard-Punkt — Brocard Punkte sind spezielle Punkte im Dreieck; benannt nach dem französischen Mathematiker Henri Brocard (1845−1922). Brocard wurde am bekanntesten für den folgenden Satz: In einem Dreieck ΔABC mit den Seiten a,b,c gibt es genau einen Punkt P… … Deutsch Wikipedia
Brocard — can refer to: * A legal term * Brocard points, Brocard triangle, Brocard circle, geometrical entities discovered by Henri Brocard. * Henri Brocard, a nineteenth century mathematician. * Saint Brocard, first of the priors of the Carmelite Order… … Wikipedia
Point de Brocard — Points de Brocard En géométrie, le premier point de Brocard d un triangle ABC est le point Ω tels que les angles et orientés positivement soient égaux. Le second point de Brocard du triangle est le point Ω tels que les angles … Wikipédia en Français
Brocard triangle — In geometry, the Brocard triangle of a triangle is a triangle formed by the intersection of line from a vertex to its corresponding Brocard point and a line from another vertex to its corresponding Brocard point and the other two points… … Wikipedia
Cercle de Brocard — En géométrie, le cercle de Brocard d un triangle est le cercle passant par les points de Brocard, le centre du cercle circonscrit et le point de Lemoine[1] . Il a pour diamètre le segment ayant pour extrémités le centre du cercle circonscrit et… … Wikipédia en Français
Brocard circle — In geometry, the Brocard circle (or seven point circle) for a triangle is a circle having a diameter of the line segment between the circumcenter and symmedian. It contains the Brocard points. [mathworld|urlname=BrocardCircle|title=Brocard… … Wikipedia
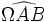
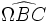 et
et 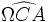 orientés positivement soient égaux.
orientés positivement soient égaux.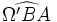
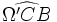 et
et 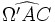 orientés positivement soient égaux.
orientés positivement soient égaux.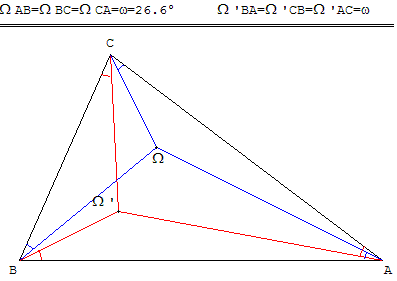
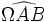
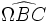
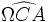
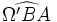
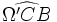 et
et 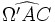 sont égaux à l'angle de Brocard du triangle, noté ω et qui peut être calculé à partir de la formule :
sont égaux à l'angle de Brocard du triangle, noté ω et qui peut être calculé à partir de la formule :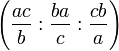 et celles du second point de Brocard sont
et celles du second point de Brocard sont 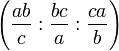 .
.