- Notation polonaise
-
Notations infixée, préfixée, polonaise et postfixée
La notation infixée est la forme d'écriture standard des expressions mathématiques dans laquelle les opérateurs sont écrits entre les opérandes, par exemple 2 + ( 5 - 3 ).
La notation préfixée est une forme d’écriture dans laquelle les opérateurs sont écrits à gauche des opérandes.
La notation polonaise est une notation préfixée inventée par le mathématicien polonais Jan Łukasiewicz en 1920[1], et qui évite l'utilisation de parenthèses. C'est la forme la plus répandue de notation préfixée en informatique et en mathématiques de par sa grammaire simple et sa concision.
La notation postfixée place les opérateurs à droite des opérandes. Elle est aussi appelée notation polonaise inverse.
Sommaire
Exemple de notation préfixée
Le langage de programmation Lisp utilise une notation préfixée, avec des parenthèses permettant de mettre un nombre indéterminé d’opérandes.
L’expression usuelle 3 * (4 + 5 + 6) se note (* 3 (+ 4 5 6)).
L’expression est interprétée en remplaçant successivement l’expression entre parenthèses par le résultat de l’opérateur écrit à gauche agissant sur les opérandes écrits à sa suite :
- (* 3 (+ 4 5 6)) => (* 3 15) => 45.
Exemple de notation polonaise
En calcul des propositions, Lukasiewicz introduisait :
-
- N pour le « non »
 ;
; - C pour l'implication
 ;
; - A pour le « ou »
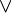 ;
; - E pour l'équivalence
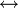 .
.
- N pour le « non »
On a par exemple :
-
- CpAqm :
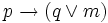
- ACpqm :
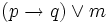 .
.
- CpAqm :
Exemple de notation postfixée
Le langage PostScript, à l’instar des calculatrices scientifiques Hewlet-Packard, utilise une notation postfixée, qui de plus peut se passer de parenthèses, les opérateurs ayant un nombre fixe d’opérandes. L’expression 3 * (4 + 5 + 6) s’écrit alors 3 4 5 add 6 add mul.
Lorsque l'interpréteur rencontre un opérande, il l'empile. Lorsqu'il rencontre un opérateur, il l'exécute sur les opérandes empilés et met le résultat de l'opération sur la pile. Ainsi, quand il rencontre l’opérateur add, il prend les deux nombres du haut de la pile et les remplace par leur somme. Il fait de même pour la multiplication avec l’opérateur mul. La pile aura donc successivement le contenu suivant :
- (3) >> (3 4) >> (3 4 5) > add > (3 9) >> (3 9 6) > add > (3 15) > mul > (45).
Analogue en langage naturel
La notation préfixée de l’expression 3 * (4 + 5 + 6) est analogue à l’expression en langage naturel : «le produit de 3 et de la somme de 4, 5 et 6).
L’analogue en langage naturel de la notation postfixée serait assez confus... : « prendre le nombre 3, puis les nombres 4 et 5, dont on calculera la somme, à laquelle on ajoutera 6, puis multiplier le premier nombre avec le résultat »...
Notes et références
- ↑ Dupas JJ, la notation polonaise, Tangente n° 120, janvier-février 2008, p30-31
Voir aussi
Article connexe
Catégories : Symbole mathématique | Calculatrice électronique
Wikimedia Foundation. 2010.
