Needleman-Wunsch

L'algorithme de Needleman-Wunsch effectue un alignement global maximal de deux chaînes de caractères (appelées ici A et B). Il est couramment utilisé en bioinformatique pour aligner des séquences de protéines ou de nucléotides. L'algorithme a été présenté en 1970 par Saul Needleman et Christian Wunsch dans leur publication A general method applicable to the search for similarities in the amino acid sequence of two proteins, J Mol Biol. 48(3):443-53.

L'algorithme de Needleman-Wunsch est un exemple de programmation dynamique, tout comme l'algorithme de Levenshtein auquel il est apparenté. Il garantit de trouver l'alignement de score maximal. Ce fut la première application de la programmation dynamique pour la comparaison de séquences biologiques.

Les scores pour les caractères alignés sont spécifiés par une matrice de similarité. Ici, S(i,j) est la similarité des caractères i et j. Elle utilise une 'pénalité de trou', appelée ici d.

Par exemple, si la matrice de similarité était

alors l'alignement:

  AGACTAGTTAC
  CGA---GACGT

avec une pénalité de trou de -5, aurait le score suivant :

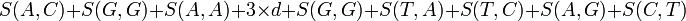
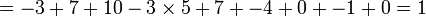
Pour déterminer l'alignement de score maximal, un tableau bidimensionnel, ou matrice est utilisé. Cette matrice est parfois appelée matrice F, et ses éléments aux positions (i, j) sont notés F_ij. Il y a une colonne pour chaque caractère de la séquence A, et une ligne pour chaque caractère de la séquence B. Donc, si on aligne des séquences de taille n et m, le temps d'exécution de l'algorithme est O(nm), et l'espace mémoire utilisé est O(nm). (Cependant, il existe une version modifiée de l'algorithme, qui utilise un espace mémoire en O(m + n), mais a un temps d'exécution plus long. Cette modification est en fait une technique générale en programmation dynamique ; elle fut introduite dans l'algorithme d'Hirschberg).

Au fur et à mesure de la progression de l'algorithme, F_ij se verra assigner le score optimal pour l'alignement des i premiers caractères de A avec les j premiers caractères de B. Le principe d'optimalité est appliqué comme suit.

  Base:
  F0j = d * j
  Fi0 = d * i
  Recursion, basée sur le principe d'optimalité :
  Fij = max(Fi − 1,j − 1 + S(Ai,Bj),Fi,j − 1 + d,Fi − 1,j + d)

Le pseudo-code de calcul de la matrice F est donné ici :

  for i=0 to length(A)-1
    F(i, 0) ← d*i
  for j=0 to length(B)-1
    F(0,j) ← d*j
  for i=1 to length(A)
    for j = 1 to length(B)
    {
      Choice1 ← F(i-1,j-1) + S(A(i), B(j))
      Choice2 ← F(i-1, j) + d
      Choice3 ← F(i, j-1) + d
      F(i, j) ← max(Choice1, Choice2, Choice3)
    }

Une fois que la matrice F est calculée, on voit que l'élément (i, j) correspond au score maximum pour n'importe quel alignement. Pour déterminer quel alignement fournit ce score, il faut partir de cet élément (i, j), et effectuer le 'chemin inverse' vers l'élément (1,1), en regardant à chaque étape à partir de quel voisin on est partis. S'il s'agissait de l'élément diagonal, alors A(i) et B(i) sont alignés. S'il s'agissait de l'élément (i-1,j), alors A(i) est aligné avec un trou, et s'il s'agissait de l'élément (i, j-1), alors B(j) est aligné avec un trou.

  AlignmentA ← ""
  AlignmentB ← ""
  i ← length(A) - 1
  j ← length(B) - 1
  while (i > 0 AND j > 0)
  {
    Score ← F(i, j)
    ScoreDiag ← F(i - 1, j - 1)
    ScoreUp ← F(i, j - 1)
    ScoreLeft ← F(i - 1, j)
    if (Score == ScoreDiag + S(A(i), B(j)))
    {
      AlignmentA ← A(i) + AlignmentA
      AlignmentB ← B(j) + AlignmentB
      i ← i - 1
      j ← j - 1
    }
    else if (Score == ScoreLeft + d)
    {
      AlignmentA ← A(i) + AlignmentA
      AlignmentB ← "-" + AlignmentB
      i ← i - 1
    }
    otherwise (Score == ScoreUp + d)
    {
      AlignmentA ← "-" + AlignmentA
      AlignmentB ← B(j) + AlignmentB
      j ← j - 1
    }
  }
  while (i > 0)
  {
    AlignmentA ← A(i) + AlignmentA
    AlignmentB ← "-" + AlignmentB
    i ← i - 1
  }
  while (j > 0)
  {
    AlignmentA ← "-" + AlignmentA
    AlignmentB ← B(j) + AlignmentB
    j ← j - 1
  }

Liens externes

• [1] Algorithme de Needleman-Wunsch en java.

Voir aussi

• Alignement séquentiel
• Programmation dynamique

• Portail de la biologie cellulaire et moléculaire