Méthode de Culmann

Méthode de Culmann
Cas schématique d'un problème solvable par la méthode de Culmann

La méthode de Culmann est une méthode de statique graphique inventée par Karl Culmann et qui est utilisée dans le cas de problèmes à quatre forces dont les directions sont connues, une force étant complètement caractérisée. Il s'applique lorsque les forces ne sont pas toutes parallèles ; si les forces sont toutes parallèles, on utilise la méthode du dynamique et du funiculaire.

Principe

Résolution du problème par la méthode de Culmann

La méthode consiste à regrouper les forces deux à deux, les deux forces d'un groupe n'étant pas parallèles. On travaille alors avec la résultante de chaque groupe de force : on se ramène alors à un problème à deux forces d'une part (pour les résultantes), et à un problème à trois forces d'autre part (pour chaque couple et sa résultante).

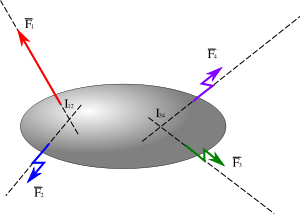
Considérons un objet soumis à quatre forces \vec{\mathrm{F}}_1, \vec{\mathrm{F}}_2, \vec{\mathrm{F}}_3 et \vec{\mathrm{F}}_4, telles que

  • \vec{\mathrm{F}}_1 est totalement connue, et l'on connaît les directions des trois autres forces ;
  • \vec{\mathrm{F}}_1 et \vec{\mathrm{F}}_2 sont sécantes en I12, et
  • \vec{\mathrm{F}}_3 sont \vec{\mathrm{F}}_4 sécantes en I34.

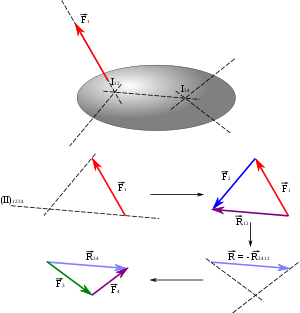
On choisit les deux couples

  • (\vec{\mathrm{F}}_1, \vec{\mathrm{F}}_2), dont la résultante est \vec{\mathrm{R}}_{12}, et
  • (\vec{\mathrm{F}}_3, \vec{\mathrm{F}}_4) dont la résultante est \vec{\mathrm{R}}_{34}.

On peut donc considérer que l'on a un objet soumis à deux forces. Ces forces sont donc colinéaires (voir Diagramme de forces > Système mécanique soumis à deux forces), on sait donc que \vec{\mathrm{R}}_{12} et \vec{\mathrm{R}}_{34} ont pour direction la droite (I12I34). Puisque l'on connaît \vec{\mathrm{F}}_1 et que l'on connaît les directions de \vec{\mathrm{F}}_2 et de \vec{\mathrm{R}}_{12}, on peut déterminer entièrement \vec{\mathrm{F}}_2 et \vec{\mathrm{R}}_{12} à l'aide d'un dynamique (on connaît un des côté du triangle et les directions des deux autres côtés).

On sait que \vec{\mathrm{R}}_{34} = -\vec{\mathrm{R}}_{12}, donc on connaît \vec{\mathrm{R}}_{34} ainsi que les directions de \vec{\mathrm{F}}_3 et \vec{\mathrm{F}}_4. On peut donc de même déterminer entièrement \vec{\mathrm{F}}_3 et \vec{\mathrm{F}}_4.

Applications

Méthode de Ritter : une utilisation possible de la méthode de Culmann

Cette méthode est souvent utilisée pour déterminer les efforts dans les poutres d'un treillis avec la méthode de Ritter : on isole un sous-ensemble soumis à une charge en coupant trois poutres, on a donc bien quatre forces (la charge et les efforts internes des poutres) dont on connaît les directions.

Monte-charge : autre situation pouvant se résoudre par la méthode de Culmann

Le monte-charge représenté ci-contre montre un autre exemple où l'on peut utiliser cette méthode : on connaît entièrement une force (le poids de l'objet), et l'on connaît la direction de toutes les forces (traction du câble, contacts ponctuels des roues du chariot sur le monte-charge).


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Méthode de Culmann de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Culmann-Verfahren — Das Culmann Verfahren (oft auch Vierkräfteverfahren genannt) ist ein zeichnerisches Verfahren zur Lösung von Problemen der Statik. Der Name geht auf den Pfälzer Bauingenieur Karl Culmann (1821 1881) zurück. Dieser hatte es sich zum Lebenswerk… …   Deutsch Wikipedia

  • Karl Culmann — Le Pr. K. Culmann de Zürich (1860). Karl Culmann (10 juillet 1821 à Bad Bergzabern, en Rhénanie, † le 9 décembre 1881 à Riesbach, auj. faubourg de Zurich) est un ingénieur allemand. Il enseigna le calcul des structures et la… …   Wikipédia en Français

  • Ferme En Treillis — Treillis (assemblage) Pour les articles homonymes, voir Treillis. Un treillis, ou système triangulé, est un assemblage de barres verticales, horizontales et diagonales formant des triangles, de sorte que la déformabilité est réduite lorsqu il est …   Wikipédia en Français

  • Ferme en treilli — Treillis (assemblage) Pour les articles homonymes, voir Treillis. Un treillis, ou système triangulé, est un assemblage de barres verticales, horizontales et diagonales formant des triangles, de sorte que la déformabilité est réduite lorsqu il est …   Wikipédia en Français

  • Système triangulé — Treillis (assemblage) Pour les articles homonymes, voir Treillis. Un treillis, ou système triangulé, est un assemblage de barres verticales, horizontales et diagonales formant des triangles, de sorte que la déformabilité est réduite lorsqu il est …   Wikipédia en Français

  • Treillis (assemblage) — Pour les articles homonymes, voir Treillis. Un treillis, ou système triangulé, est un assemblage de barres verticales, horizontales et diagonales formant des triangles, de sorte que la déformabilité est réduite lorsqu il est soumis à un effort …   Wikipédia en Français

  • Statique graphique — Pour les articles homonymes, voir Statique. La statique graphique est une méthode entièrement géométrique de résolution de problèmes de mécanique statiques. Elle est adaptée aux problèmes : de mécanique newtonienne ; pour l étude des… …   Wikipédia en Français

  • Diagramme de forces — En mécanique statique, et plus particulièrement celle du solide, le diagramme de forces est une méthode graphique pour déterminer l intensité de forces agissant sur un système en équilibre. Il est appelé aussi « un dynamique des… …   Wikipédia en Français

  • Diagramme De Forces — En mécanique statique, et plus particulièrement celle du solide, le diagramme de forces est une méthode graphique pour déterminer l intensité de forces agissant sur un système en équilibre. Il est appelé aussi « un dynamique des… …   Wikipédia en Français

  • Polygone des forces — Diagramme de forces En mécanique statique, et plus particulièrement celle du solide, le diagramme de forces est une méthode graphique pour déterminer l intensité de forces agissant sur un système en équilibre. Il est appelé aussi « un… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”