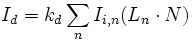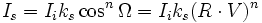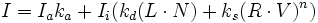Lissage Phong

Les types d'ombrage numériques
Ombrage plat
Ombrage de Gouraud
Ombrage de Phong

Aujourd'hui, le terme ombrage de Phong est utilisé à la fois pour le modèle d'illumination de Phong, et l'interpolation de Phong, deux algorithmes de traitement 3D en infographie. Tous les deux furent développés par Bui Tuong Phong.

Sommaire 1 Modèle d'illumination de Phong 1.1 Les failles du modèle de Phong 2 L'interpolation de Phong 3 Voir aussi

Modèle d'illumination de Phong

L'illumination de Phong est un modèle local, c'est-à-dire qui calcule l'intensité en chaque point, et qui combine trois éléments - la lumière diffuse (modèle lambertien), la lumière spéculaire et la lumière ambiante.

Il y a plusieurs présupposés à ce modèle : toutes les lumières sont assimilables à un point, il ne peut y avoir que des surfaces (pas de rendu en volume), et la lumière ambiante est supposée constante.

La composante diffuse, I_d est donnée par :

I_d = I_ik_dsinθ

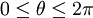
Avec I_i l'intensité de la lumière, θ l'angle entre la surface et la source de lumière et k_d le coefficient de réflexion diffuse. Plus souvent, on utilise le cosinus de l'angle entre la normale de la surface et la lumière - cette technique est plus simple à mettre en œuvre, mais revient, mathématiquement, au même.

Pour plusieurs sources lumineuses, on a :

Avec L et N des vecteurs unitaires, L_n le vecteur direction de la source de lumière n.

La composante spéculaire I_s est donnée par :

Avec n la réflectivité de la surface (un miroir parfait posséderait un n infini), Ω l'angle entre R la direction de la lumière spéculaire (réflexion parfaite du rayon lumineux par la surface) et V le vecteur vu de l'observateur, que l'on calcul en pratique par un produit scalaire, ces deux vecteurs étant normés. n détermine donc l'étalement de la tâche lumineuse dût à la spécularité, pour un n grand la tâche est très concentrée.

C'est une première faille du modèle de Phong : on ne peut appliquer ici la radiosité.

En combinant la lumière diffuse et spéculaire, on obtient un modèle globalement suffisant, mais, pour simuler la lumière résiduelle, Phong ajouta une troisième composante, la lumière "ambiante", indépendante du point de vue ou de l'objet.

La composante ambiante I_g est une constante, donnée par :

I_g = I_ak_a

Ce qui donne le modèle général d'illumination de Phong :

Les failles du modèle de Phong

• Comme il est dit plus haut, la composante spéculaire se base sur deux vecteurs directionnels, l'observateur et la lumière, et interdit toute radiosité du modèle.
• Ce modèle est purement empirique, n'est fondé sur aucune théorie physique, mais uniquement sur les observations de Phong
• Ce modèle ne prévoit pas la diffusion de la lumière avec la distance

L'interpolation de Phong

Cette méthode, à mettre en parallèle avec l'interpolation de Gouraud, produit de bons résultats de rendus, souvent plus réalistes que son prédécesseur.

Le principal problème de l'ombrage de Gouraud, c'est qu'il ne calcule que les sommets (vertex) des polygones : une source lumineuse spéculaire placée au centre d'un triangle n'apparaîtra pas. Ce problème est réglé avec l'interpolation de Phong.

Soient trois sommets distincts : v₁, v₂ et v₃, ayant pour vecteurs unitaires normaux n₁, n₂ et n₃. Comme pour l'interpolation de Gouraud, celle-ci se fait de façon linéaire sur toute la surface du triangle v₁v₂v₃, seulement elle se fait depuis les trois vecteurs normaux des sommets, c'est-à-dire que nous interpolons en fait les vecteurs normaux au lieu des couleurs.

À la différence de l'interpolation de Gouraud cependant, le calcul ne se fait pas sur 3 points par surface, mais pour tous les points d'une surface - ou plus raisonnablement, sur plusieurs subdivisions de points. Cette méthode, bien plus lente, est parfois traitée par le matériel directement, via les shaders.

Voir aussi

• Interpolation de Gouraud
• Bui Tuong Phong

• Portail de l’informatique